Σ計算のルール

前回のΣ計算の基本ではΣ(シグマ)はどのようなものかというのを高校でやっていない人向けに解説しました。今回はもう少し踏み込んで、Σ計算のその他のルールについてみていきたいと思います。

 

まず例題からです。

 

例題

ある散剤を開発するにあたり主薬に対して賦形剤Xと、結合剤Yを組み合わせてどれくらいの量がいいかを調べた。以下は5つのサンプルデータである。

 

 

例題を出しておきながら、今回は答えなるものがありません。このデータを使ってΣ計算のルールを見ていきます。

 

まず、「総量の合計」は30ですね。そして、これは賦形剤Xと結合剤Yの全てのデータを足し合わせたもの(15+15)と一致します。このことから、今のことをΣを用いて表すと以下のように書くことができます。

 

 

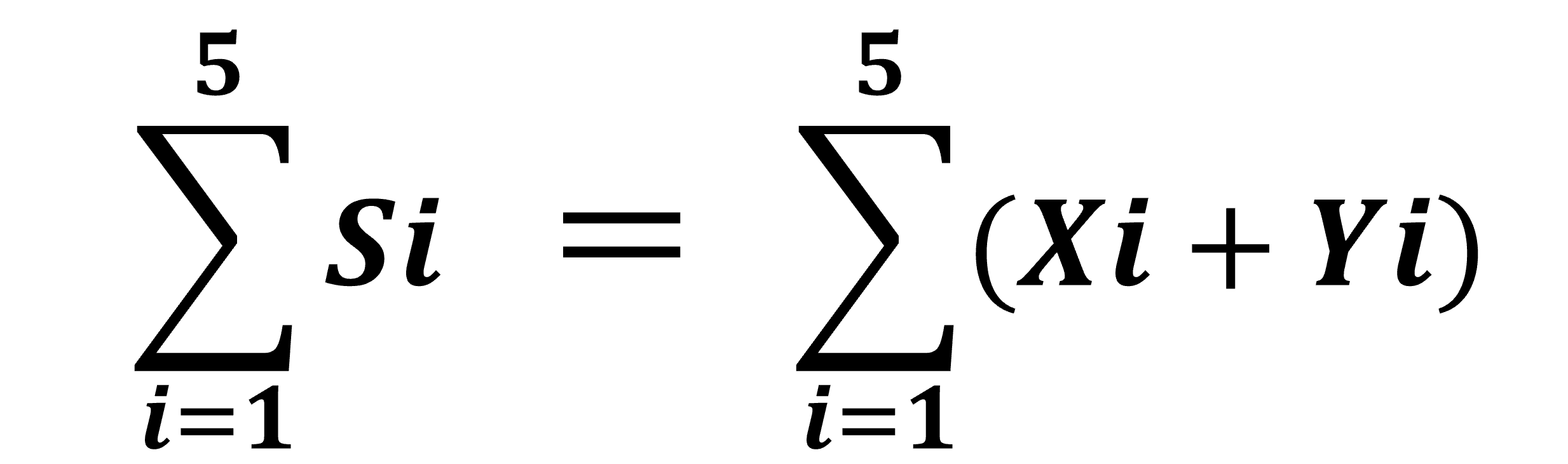
ここまでは問題ないかと思います。ではこの例題を頭にいれつつ、以下のΣ計算のルールを見ていきます。

 

• 足し算の総和の分解
• 引き算の総和の分解
• 変数ではなく定数の場合のΣ計算
• 定数+変数のΣ計算
• 定数×変数のΣ計算

 

足し算の総和の分解

 

 

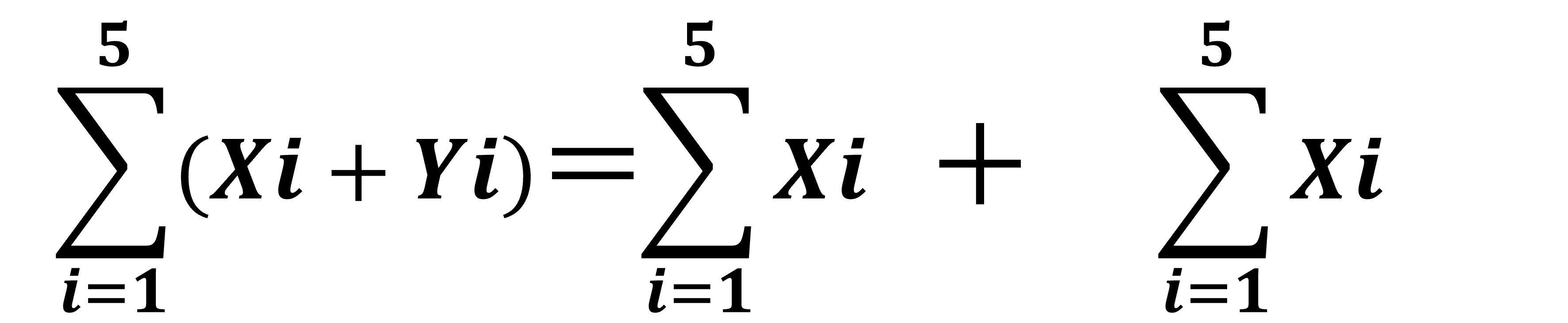
足し算の総和は分解することができます。賦形剤Xの総和が15、結合剤Yの総和が15と独立して計算したものを足したものが、総量30と一致することからもわかると思います。

 

引き算の総和の分解

 

 

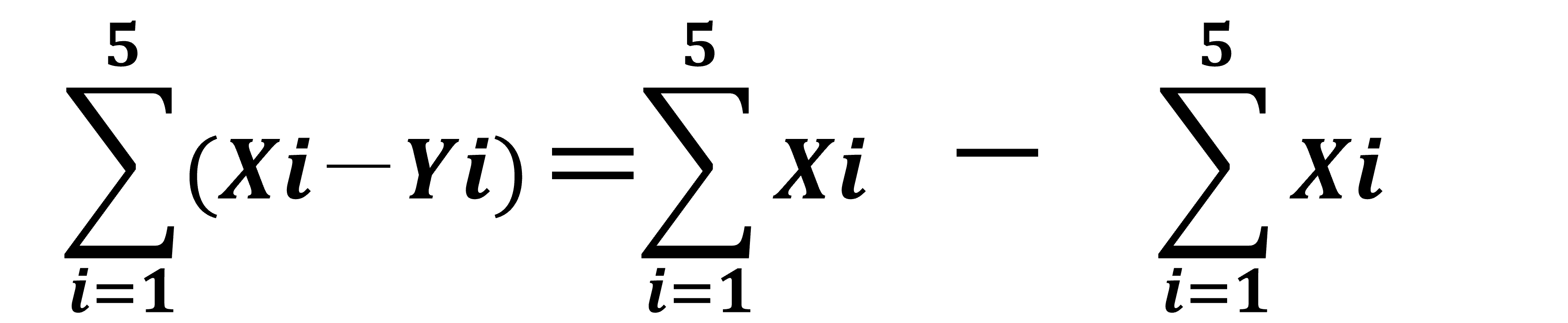
今回のデータにおいてはマイナスのデータが出てきてしまうので現実的ではありませんが、ルールとしては直感的に受け入れてもらえると思います。

 

変数ではなく定数の場合のΣ計算

 

 

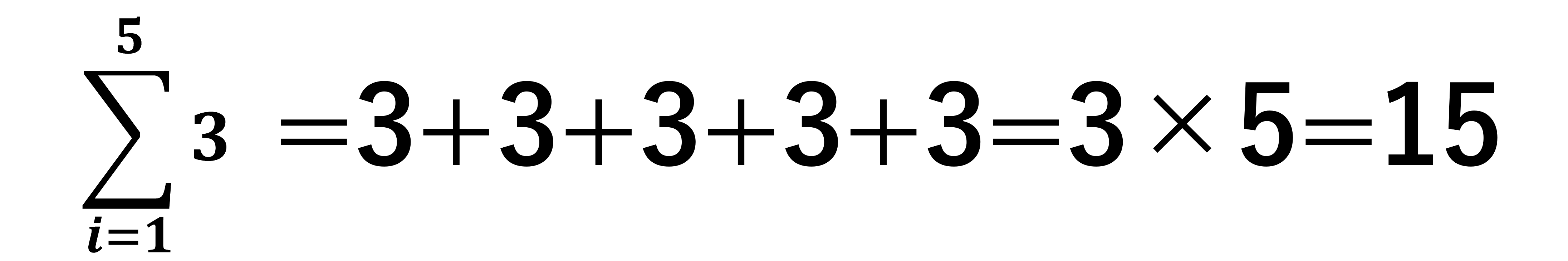
今までΣの中身は変数で変わるものでしたが、定数の場合は上のようになります。イメージとしてはデータ1からデータ5までが全て3であるため、それらを足し合わせると3+3+3+3+3=15となるイメージです。

 

定数+変数のΣ計算

 

 

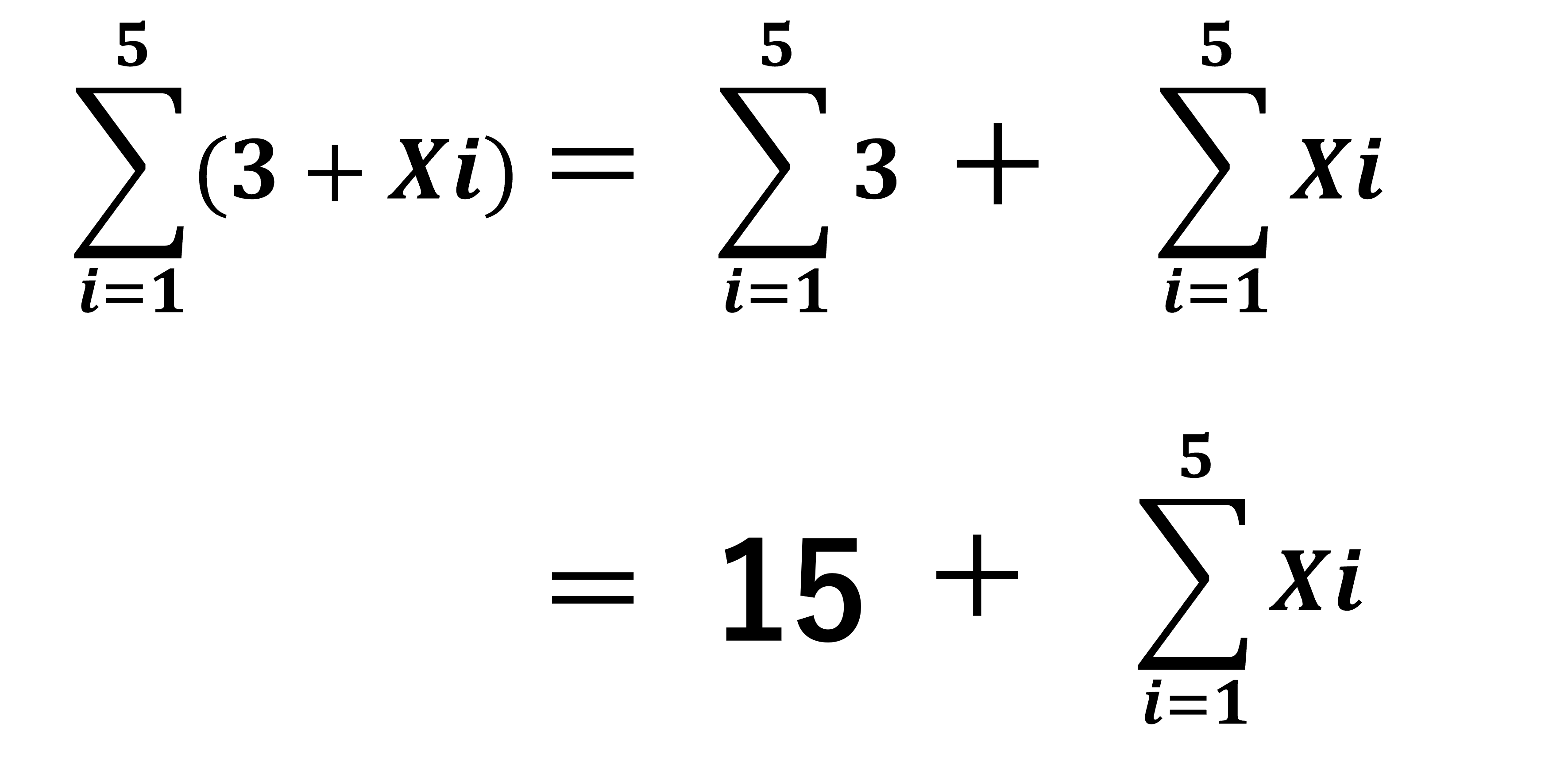
今までのルール1とルール3の応用です。まずルール1にのっとり、定数部分と変数部分をわけます。

 

次に定数部分はルール3が適応することで先ほどの15となります。これを変数部分と足し合わせるという形に分解することができました。

 

定数×変数のΣ計算

 

 

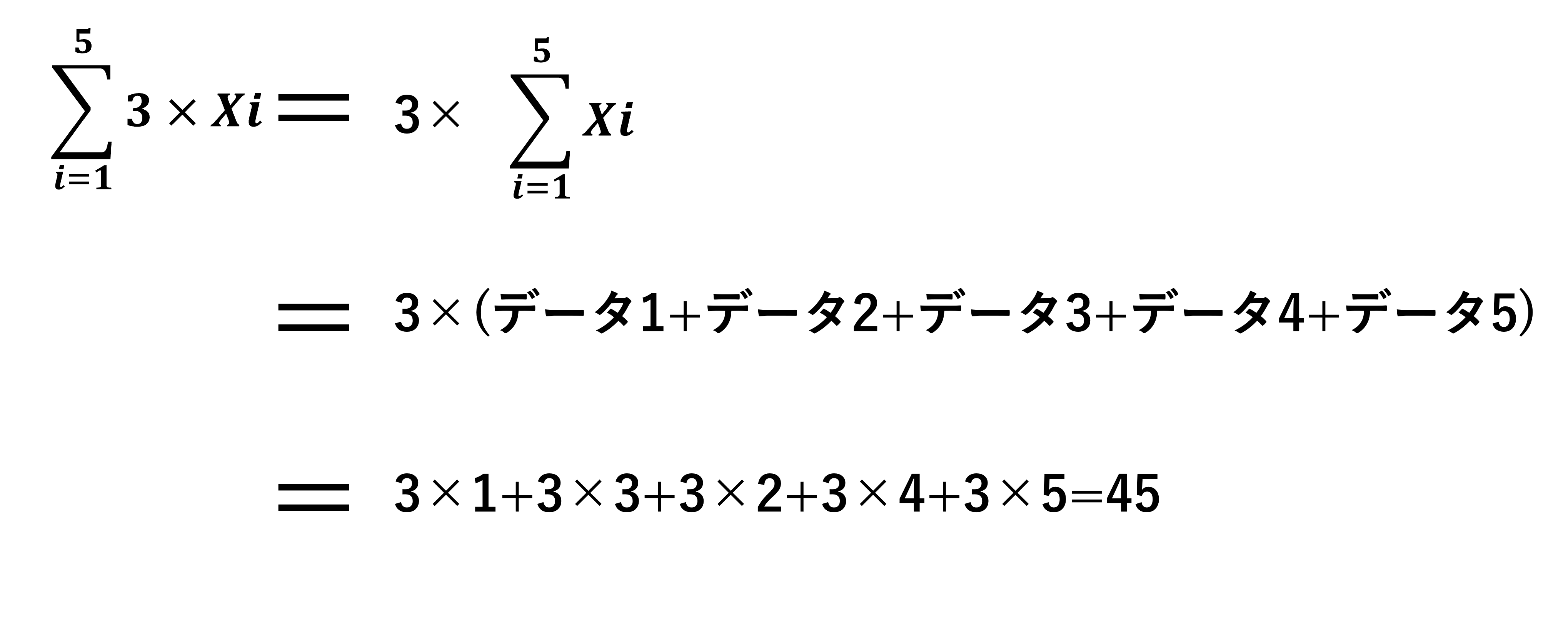
定数×変数のΣ計算は定数をΣの外側に出すことができます。例えば3×賦形剤XiのΣ計算では、3×Σxiという形にできます。

 

いまいちピンとこない人はΣ3×Xiを考えると、Xiのデータを3倍したものを足してねという意味となります。つまり3+9+6+12+15=45を意味しているわけです。

 

一方で3×Σxiは、Σxiをまず計算すると15です。それを3倍するため、3×15=45となるため先ほどのΣ3×Xiの計算結果と一致します。

 

これらのΣ計算のルールを理解できていれば、少なくとも薬学部の統計学では苦労しないと思うのでしっかりと理解して、すぐに変換できるように慣れておきましょう。

 

まとめ

• 薬学部の統計学では、Σ計算のルールをしっかり理解してすぐに変換できるようになれよう