標準正規分布と性質

前回の正規分布の式とグラフでは、正規分布についてみました。今回は標準正規分布についてみていきたいと思います。今回は特にいままでの知識が必要になってくるので、わからない方は復習をしつつ読んでください。

 

 

標準正規分布

前回の復習をすると、正規分布の式は以下のようにあらわされました。

 

 

この式のうち平均が0で標準偏差が1の時、「xは平均が0で標準偏差が1の正規分布に従う」と統計学では表現するという話を前回しました。

 

しかし平均が0で標準偏差が1の時は、「xは標準正規分布に従う」と統計学では言います。そして、代入すればわかると思いますが標準正規分布の式は以下のように少しシンプルになります。

 

 

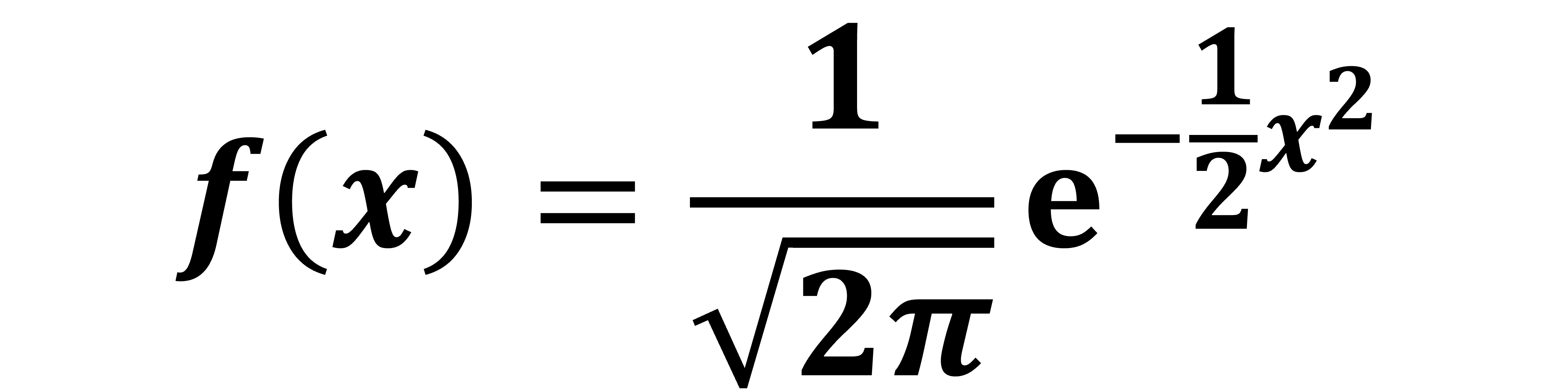
ところで、そんな都合よく平均が0で標準偏差が1の時なんてあるのかと思う方もいるかもしれませんが、それがあるんです。

 

ヒントというか、ほぼ正解ですが基準値がまさにそうです。これも復習になりますが基準値は以下のような特徴を持つのでした。

 

• 満点が何点であっても、その基準値の平均は0、標準偏差は1となる。
• どのような単位であっても、その基準値の平均は0、標準偏差は1となる。

 

まさに、平均が0で標準偏差が1ですね。つまり基準値に直した衛生のテストは標準正規分布に従うことになります。

 

 

標準正規分布の性質

標準正規分布は平均が0と標準偏差が1以外にも次の大事な性質を持ちます。

 

• 平均から標準偏差1個以内のデータの相対度数は0.6826(約70%がこの中に入る)
• 平均から標準偏差2個以内のデータの相対度数は0.9544(約95%がこの中に入る)

 

すでに標準偏差を用いて、データの特殊性を評価するでも解説済みですが、標準偏差2個以内にほぼすべてのデータが入ってしまうというのはデータを判断するうえでとても大事な性質となります。

 

 

有意である、有意でないとは

よく製薬メーカーの勉強会などに出ると、「新薬○○の治療効果は、従来の薬●●と比べて有意なデータが得られました。」などと説明がされることがあります。では統計学における有意である、有意でないというのはどういうことを意味するのでしょうか？

 

統計学では、めったに起こらないほど大きな値であることを有意に大きいと表します。例えば先ほどの正規分布における標準偏差±2より外側である左右2.5%のデータは有意に大きい、あるいは有意に小さいと言えるでしょう。このように極端に大きな値や小さい値の場合、統計学では「有意である」と表現します。

 

これに対して、標準偏差±2より内側は95%であり、よく起こる値であると言えます。このことを統計学では、「有意でない」と表現します。

 

正規分布の性質

では次に正規分布の性質も見てみましょう。標準正規分布では平均が0で標準偏差が1でしたが、これを正規分布に変換するには標準正規分布のデータを加工する必要があります。

 

つまり、標準正規分布の全てのデータに一定数をかけて、そのあと一定数を加えることで加工することができます。データを加工すると平均値や標準偏差には以下のような影響がありました。

 

• 全データに一定数をかけて新しいデータを作ると、平均値と標準偏差はかけた数字だけ増える。
• 全データに一定数を加えて新しいデータを作ると、平均値は加えた数字だけ増え、標準偏差には影響を与えない

 

これも別ページ、データに一定数を加えた時の平均値や標準偏差への影響やデータに一定数をかけた時の平均値や標準偏差への影響で解説済みなので、必要であれば復習してください。

 

具体的な例をあげると、標準正規分布のデータに、6をかけて、5加えたとします。この時の平均値や標準偏差は先ほどのデータ加工の影響をもとに以下のように変化します。

 

• 6をかける；平均値は0×6=0、標準偏差は±1×6=±6
• 5を加える；平均値は0+5=5、標準偏差は±6+5=−1、+11

 

 

つまり、ヒストグラムは左右に6倍だけ広がって、右に5進んだヒストグラムに加工されたことがわかります。さらに、これをもとに先ほどの標準正規分布の特性を考えると、以下のようになります。

 

• 平均から標準偏差1個以内のデータの相対度数は0.6826(約70%がこの中に入る)→−1〜＋11までにデータの約70%が入る。

 

以上のことから、平均値μ(ミュー)、標準偏差σ(シグマ)における正規分布の特性を以下のように言うことができます。

 

• μ±σの範囲のデータの相対度数は0.6826(約70%がこの中に入る)
• μ±2σの範囲のデータの相対度数は0.9544(約95%がこの中に入る)

 

今までの知識がだいぶ積み重なってきたのが実感できる内容だったかと思います。

 

まとめ

• 平均が0で標準偏差が1の時は、xは標準正規分布に従う
• 正規分布の特性としてμ±σの範囲のデータの相対度数は0.6826(約70%がこの中に入る)、μ±2σの範囲のデータの相対度数は0.9544(約95%がこの中に入る)