標準偏差、基礎編

前回の分散とは？では分散についてみました。分散はデータのバラつき具合がわかるという話をしましたが、少し欠点もあります。それを補うのが標準偏差です。標準偏差と言えば、統計学を代表するワードであり、統計学アレルギーの方でも何度も聞いたワードでしょう。今回は標準偏差について見ていきたいと思います。

 

 

分散の欠点

前回も平均値の欠点から入りましたが、分散にも欠点が2つあります。

 

第一に、バラつきを表す数値にしては大きすぎるという点です。前回の偏差の値を改めて見てみましょう。

 

• 21−28.3=−7.3
• 19−28.3=−9.3
• 20−28.3=−8.3
• 18−28.3=−10.3
• 36−28.3=7.7
• 39−28.3=10.7
• 30−28.3=1.7
• 35−28.3=6.7
• 32−28.3=3.7
• 33−28.3=4.7

 

偏差は大きくても±10の範囲で収まっています。しかし、算出した分散は57.21とかなり大きい数字となっています。

 

 

第二の欠点は単位が変わっているということです。薬学部の皆様であれば、物理や薬剤で単位をそろえることがいかに重要かということを体感していると思います。統計学も同じです。分散を求めるにあたって、年齢を二乗しているので、単位は歳の二乗となってしまっています。これは元のデータは歳であったためおかしくなってしまっていることがわかります。

 

これを解消するにはどうすればよいでしょうか？

 

二乗をもとに戻すためにルート√をとればよいのです。57.21の√をとると、7.56です。これであれば、先ほどの問題点も解消されています。このように分散の√をとったものを標準偏差と呼びます。標準偏差はstandard deviation；SDとも略されることがあり、統計学においてはかなり重要なポジションをしめています。

 

平均値と標準偏差

では今回の年齢におけるデータについて平均値と標準偏差を交えてまとめてみます。

 

平均年齢は28.3歳でしたが、それがどれくらいのバラつきがあるかがわかりません。それがわかるのが標準偏差であり、前後に約7.56歳ほど散らばっている。このように解釈できます。

 

 

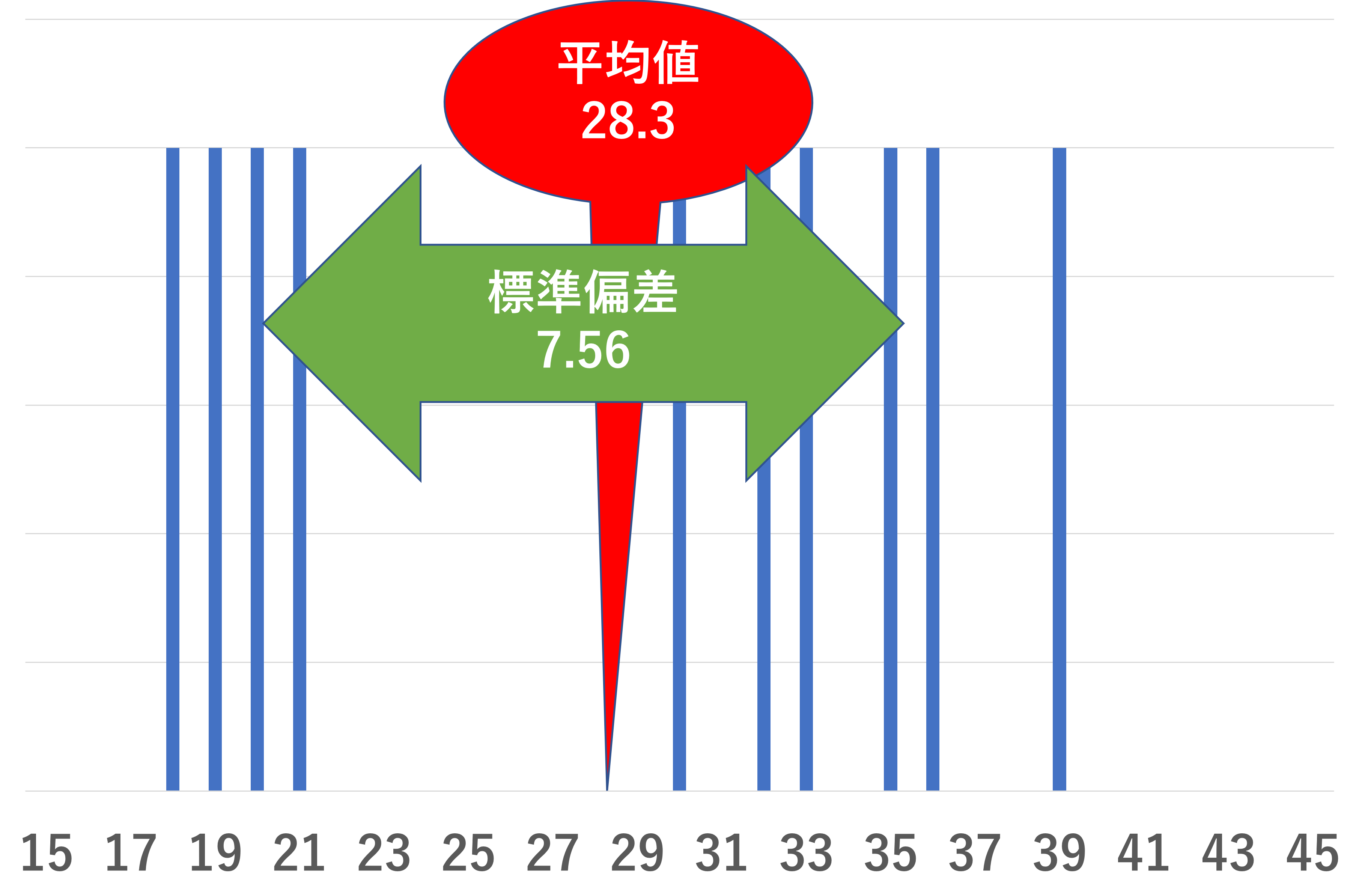
標準偏差は最小値が0であり0であれば散らばりが全くない、つまり全て同じデータということができます。逆に標準偏差が大きいほどデータの散らばりが大きいといえます。

 

どうでしょうか？標準偏差について少し理解が進んだでしょうか？次回は標準偏差の例題編でさらに理解を深めたいと思います。

 

まとめ

• 分散の欠点を解消するために√をとったものが標準偏差であり統計学ではかなり重要。