

Sponsored Link
標本平均とは
前回の母標準偏差の出し方では、母標準偏差についてみました。今までは母集団からデータを一個抽出した場合を見ましたが、これが複数個ある場合はどうなるでしょうか?今回は標本平均についてみてみます。

標本平均
母平均を推定するにあたって、一個のデータ(標本)から推定するよりは、複数個データがあった方がいいというのは、ここまで統計学をやってきた皆さんであれば直感的にわかるかと思います。なぜなら、偶然に起きるデータの散らばりをなるべくなくして、より実際の値に近づけるからです。
では、複数個データがある場合はどうするのか?これも今まで統計学をやってきた皆さんに対しては愚問ですね。データの合計の平均をとればいいですね。このようにして観測されたデータの平均値を標本平均と呼び、以下のような式で表されます。
- 標本平均=観測されたデータの合計÷観測データ数

では、ここでまた例題を見てみましょう。
ドラえも〇の四次元ポケットがあったとする。四次元ポケットの中に、「1」、「2」、「3」、「4」、「5」と書かれたくじが無限に入っていて、どの数字も出る確率は20%であるという。この四次元ポケットから、くじを引く作業を行う。
Sponsored Link
Sponsored Link
まずこのくじの母平均を出してみましょう。
階級値×相対度数の合計=平均値であるため、1×0.2+2×0.2+3×0.2+4×0.2+5×0.2=3。よって母平均は3となります。
次にこの四次元ポケットから2回くじを引いた場合を考えてみましょう。1回目にくじを引いたときに「1」、「2」、「3」、「4」、「5」の5通り、2回目にくじを引いた時も「1」、「2」、「3」、「4」、「5」の5通りがあるので、すべてで25通りが均等に出てくることになります。
標本平均=観測されたデータの合計÷観測データ数であるため、例えば「1」と「1」であるならば、(1+1)/2=1と標本平均なります。これを全ての25通りで標本平均を出すと以下の図のようになります。
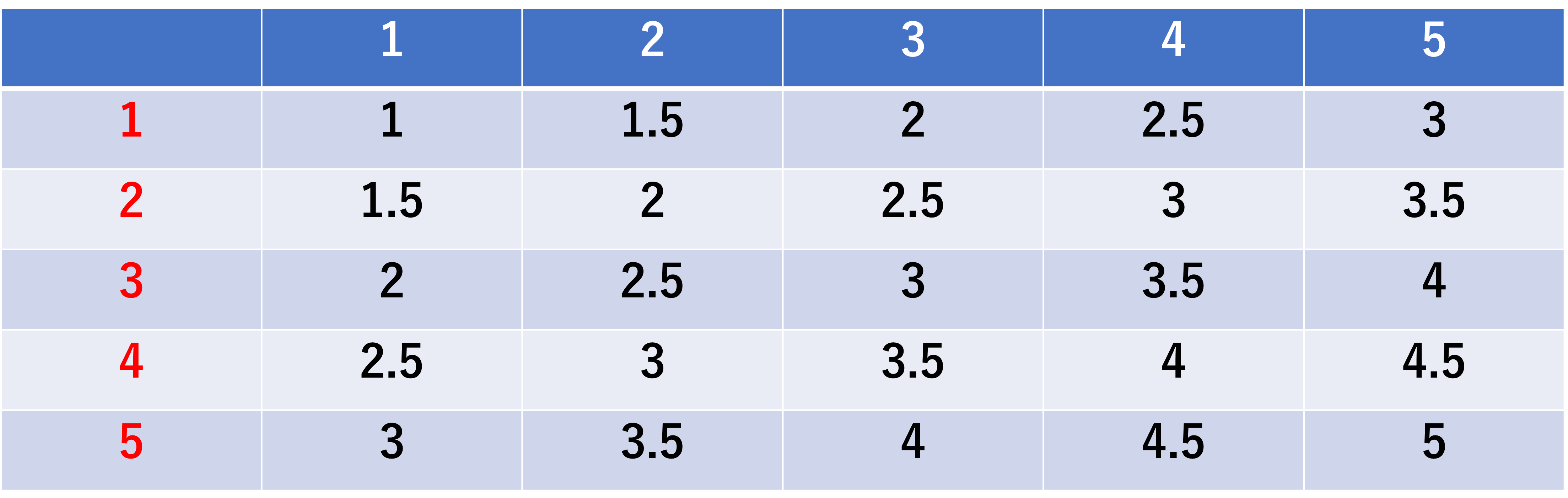
つまり1から0.5きざみで5までの数字が出てくることになりますが、この時に出てくるデータの回数は異なり以下のようになっています。
- 1;1
- 1.5;2
- 2;3
- 2.5;4
- 3;5
- 3.5;4
- 4;3
- 4.5;2
- 5;1
ここでヒストグラムを考えてみます。母集団のヒストグラムは全ての数字が出てくる可能性が20%だったので平らなヒストグラムとでしたが、くじ引き2回のヒストグラムでは山のようなヒストグラムとなり、しかも母平均3の周辺に相対度数が高くなっているのがわかるかと思います。

このように1つの母集団からn個のデータを観測して標本平均を作ると、nが大きいほど標本平均は母平均に近い数値をとる可能性が高くなります。
まとめ
- 1つの母集団からn個のデータを観測して標本平均を作ると、nが大きいほど標本平均は母平均に近い数値をとる可能性が高くなる
