平均値と中央値の違い

前回の度数分布表とヒストグラム、例題編までで、度数分布表やヒストグラムを極めました。

 

 

度数分布表やヒストグラムはデータの特徴をわかりやすくするのに役立ちますが、少し欠点もあります。それは度数分布表やヒストグラムを見て、データの特徴のとらえ方が人によって違うということです。前回の例題で私は

 

• 26〜30にデータが集まっている。
• 26〜30を起点にして年齢が低い方にも高い方にも左右対称にデータが分布している。

 

といった特徴をあげました。しかし、あなたはそうとらえないかもしれません。そうなると意見の違う私とあなたが、この度数分布表やヒストグラムを議論した時にすれ違ってしまいます。そういったときに出てくるのが統計量です。統計量とはデータの特徴を1つの数字に要約したもので、平均値、分散、標準偏差などがあります。今回はそのうち平均値を見てみましょう。

 

 

平均値

平均値は皆さんが知らぬ間に習得してしまっている(？)統計量なので詳細な説明は不要かと思います。データの合計値を全データで割ったものですね。例えば前回の年齢に関するデータについて3つのチームに分けたとします。

 

 

• Aチーム；(21+19+20+18+36+39+30+35+32+33)/10=28.3
• Bチーム；(26+23+24+28+26+30+30+34+32+33)/10=28.6
• Cチーム；(27+25+21+23+27+28+26+31+36+33)/10=27.7

 

といった具合に平均値を出すことができます。

 

平均値は、その他average、meanなどとも表され、教科書によっては記号エックスバーで表されているかと思います。平均値をΣ(シグマ)を用いて表すと以下のようにあらわされます。

 

 

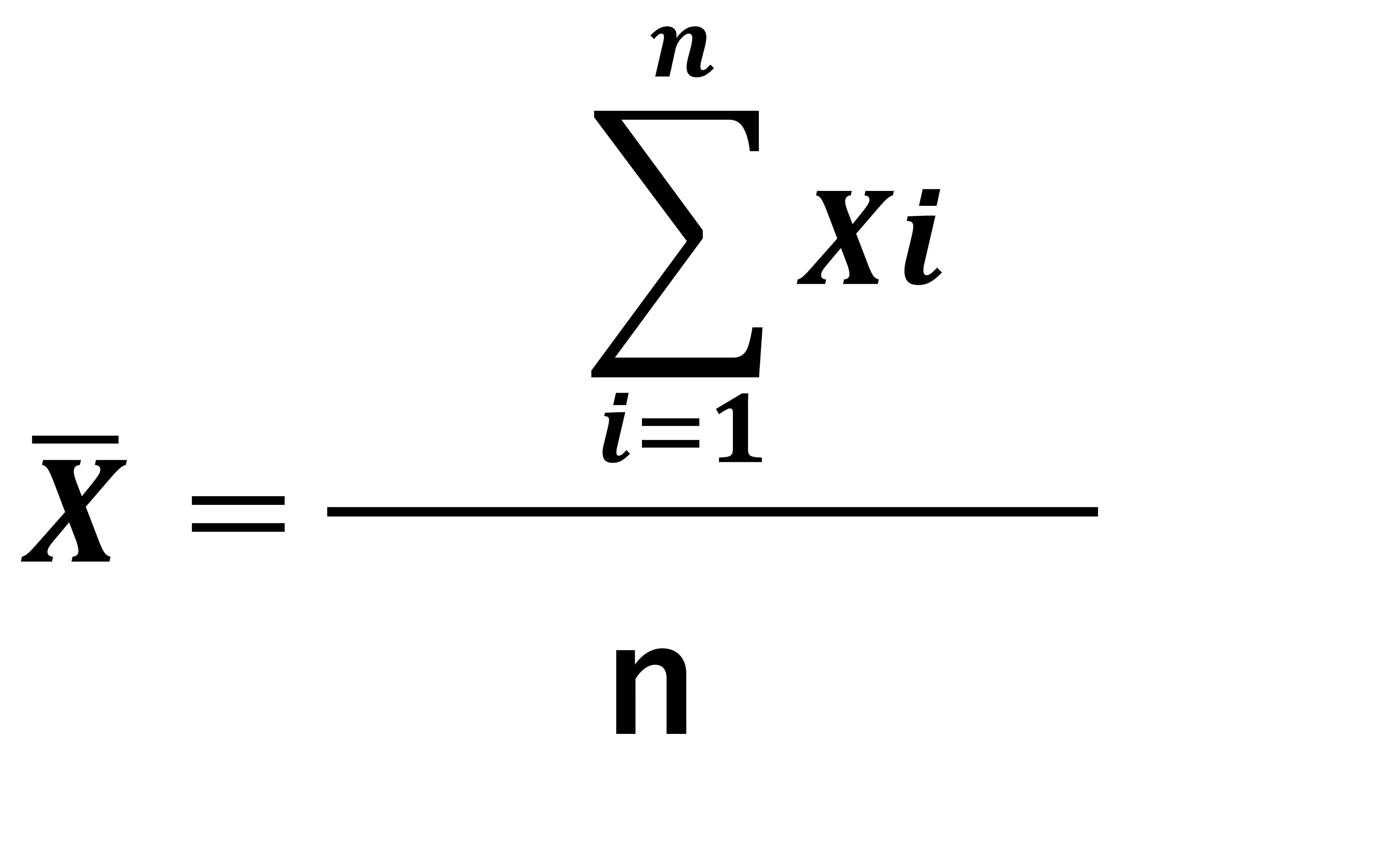
さて、それぞれのチームの平均値の結果を見てみると、Aチームは最初の数名の年齢が低いので平均値も低くなるかと思いきや、Cチームよりも平均値が上ですね。また、BチームとCチームも同じくらいかと思いきや、平均値は約1も違うことがわかりますね。

 

平均値はデータが広がって存在している中から1点全データを代表する数値として選び出したものです。そのためデータたちは平均値の近くに分布しているし、多く現れるデータはそれだけ平均値に大きな影響を与えることもわかります。

 

今回出したいわゆる平均値は、算術平均や相加平均と呼ばれるもので、その他にも幾何平均(相乗平均)や二乗平均、調和平均といった様々な平均があり、用途によって使い分けられます。とりあえず今回は従来の平均値がわかっていればOKです。

 

中央値

平均値に似た言葉に中央値がありますが違います。中央値とは、データを小さい順に並べたときに真ん中にくる値のことで、medianなどとも表され、記号ではMeやエックスウィグル(Xの上に「〜」の文字)で表されます。

 

データの個数が奇数ならばちょうど真ん中のデータが中央値、偶数の場合は真ん中の値2つの平均が中央値となります。早速、先ほどの3チームの中央値を出してみましょう。

 

まず小さい順から並び替えます。

 

• Aチーム；18、19、20、21、30、32、33、35、36、39
• Bチーム；23、24、26、26、28、30、30、32、33、34
• Cチーム；21、23、25、26、27、27、28、31、33、36

 

今回は各チームのデータが10個で偶数なので真ん中の2つの平均値が中央値となるので

 

• Aチーム；(30+32)/2=31
• Bチーム；(28+30)/2=29
• Cチーム；(27+27)/2=27

 

なんと平均値ではAチームよりBチームの方が上でしたが、中央値ではBチームよりAチームの方が上でしたね。

 

Aチームのようにデータの中に異様に大きいものや小さいものがある場合、中央値を求めるとよい場合もあります。

 

まとめ

• 平均値はデータの合計値を全データで割ったもの
• 中央値はデータを小さい順から並べたときに真ん中にくるもの