独立性の検定の計算、例題

前回の独立性の検定、帰無仮説と対立仮説では、帰無仮説と対立仮説などを見ました。今回は独立性の検定を例題とともに具体的にみていきます。

 

 

検定の手順

独立性の検定の例題の前に、検定の手順を確認します。検定は一般的に以下の手順で行われます。

 

1. 母集団を定義する
2. 帰無仮説と対立仮説を決める
3. 行う検定を選ぶ
4. 優位水準を決める
5. 標本データから検定統計量を求める
6. 求めた統計量が棄却域に入っているかを確認し結論を出す。

 

では、例題を見てみましょう。

 

 

例題

某薬学部の学生からランダムに20人を選び衛生か薬剤どちらの科目が好きかをアンケートして以下の結果が得られた。母集団の某薬学部における性別と好きな科目は関連しているかどうかを独立性の検定により推測せよ。ただし有意水準は0.05とする。

 

 

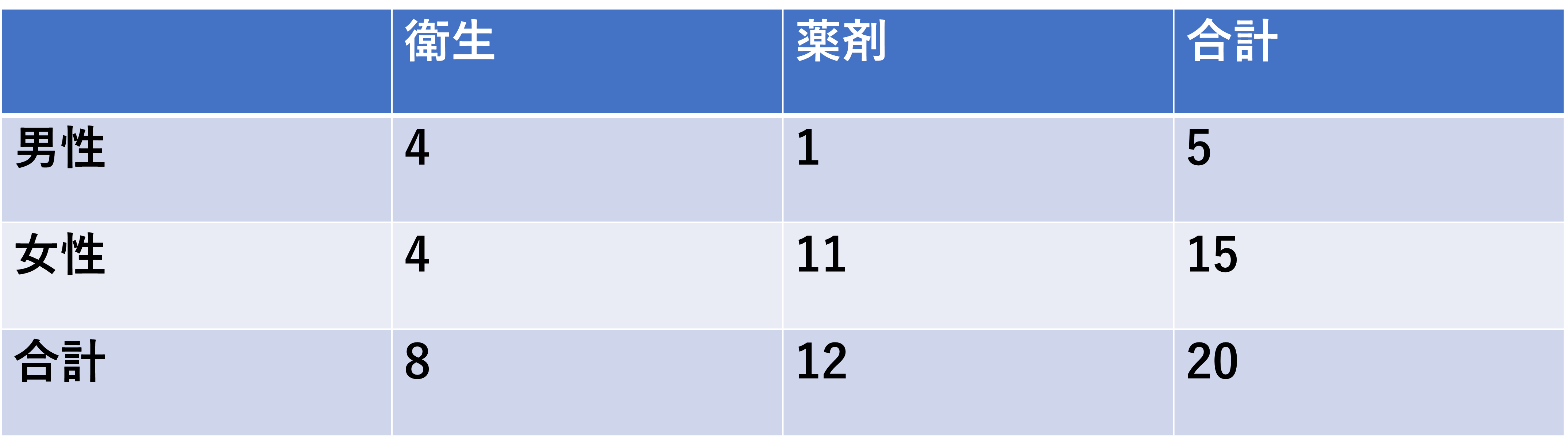
まず、検定の手順は以下の通りでした。

 

1. 母集団を定義する
2. 帰無仮説と対立仮説を決める
3. 行う検定を選ぶ
4. 有意水準を決める
5. 標本データから検定統計量を求める
6. 求めた統計量が棄却域に入っているかを確認し結論を出す。

 

しっかりやった方はわかると思いますが、別ページクラメールの連関係数と例題の例題の計算結果などを利用しているので、適宜参照してください。

 

母集団を定義する

問題文にすでに書いてありますが、母集団は某薬学部の学生となります。

 

帰無仮説と対立仮説を決める

帰無仮説と対立仮説は以下のようになります。

 

• 帰無仮説；性別と好きな科目は関連していない
• 対立仮説；性別と好きな科目は関連している

 

ここまでは前回でやったので問題ないかと思います。

 

行う検定を選ぶ

これも問題文に書いてありますが、独立性の検定です。検定では、とりあえず母集団におけるクラメールの連関係数は0として話を進めていきます。

 

そしてクラメールの連関係数が0であるならば、ピアソンのカイ二乗統計量は自由度1のカイ二乗分布に従います。なぜ自由度1のカイ二乗分布になるのかは大人の事情で割愛しますが、以下のように求められます。

 

• (カテゴリーデータAの項目数−1)×(カテゴリーデータBの項目数−1)

 

今回はカテゴリーデータAの項目を性別とすると、女性か男性の2通り。カテゴリーデータBの項目を好きな科目とすると、衛生か薬剤の2通り。つまり

 

(2−1)×(2−1)=1と求められます。

 

検定は独立性の検定の他にも、相関比が0ではないかどうか推測する相関比の検定、単相関係数が0ではないかと推測する無相関の検定などの種類があります。

 

有意水準を決める

これも問題文に書いてありますが、有意水準は0.05です。

 

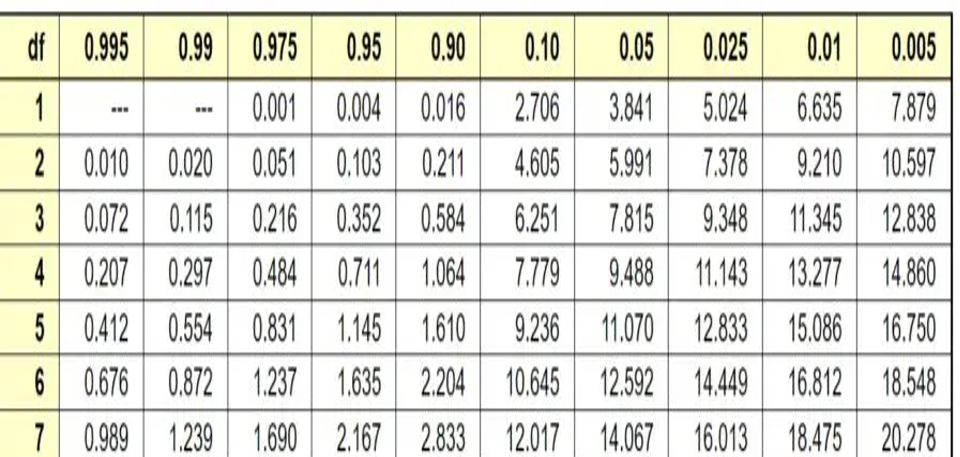
有意水準とは今回の問題の場合、カイ二乗分布表より求められる面積(確率)のことです。詳細は別ページカイ二乗分布表の読み方と例題を参考としてください。一般的には有意水準は0.05や0.01などが選ばれます。

 

 

標本データから検定統計量を求める

独立性の検定であるので、使う検定統計量はピアソンのカイ二乗統計量となります。そして前の例題ですでに求めているので、4.44となります。

 

求めた統計量が棄却域に入っているかを確認し結論を出す。

自由度1のカイ二乗分布表より、有意水準0.05は3.841以上となります。そして今回の例題における3.841以上の領域を棄却域と呼ばれます。

 

 

検定統計量が棄却域に入っているならば対立仮説は正しいとします。もし棄却域に入っていなければ、帰無仮説は誤っているとはいえないとします。

 

先ほど出した4.44は棄却域に入っています。よって、母集団のクラメールの連関係数が0より大きいとなるため、性別と好きな科目は関連しているという対立仮説は正しいという結論になります。

 

まとめ

• 独立性の検定は、母集団のクラメールの連関係数が0として話を進めていく