標準正規分布表、面積と確率

前回の正規分布の95%予言的中区間と例題までで、95%予言的中区間についてみました。今回はこれをさらに深掘りした標準正規分布表についてみていきたいと思います。

 

 

確率密度関数の面積

標準正規分布において95%予言的中区間は、−1.96〜＋1.96という話をしました。この範囲にデータの95%が存在しているということになります。つまり、−1.96〜＋1.96と標準正規分布のグラフで囲まれた面積が95%(0.95)あるということになります。

 

では、少し発展させて標準正規分布の横軸の範囲である±∞と標準正規分布のグラフで囲まれた面積はいくつになるでしょうか？

 

標準正規分布などの確率密度関数のグラフと横軸で囲まれた面積は1となります。これは、さきほどの95%予言的中区間がわかっていればなんということはないと思います。

 

 

この最大面積1のうち、横軸の値からどれくらいの面積を占めているかがわかるものが標準正規分布表です。

 

横軸が1.96の場合を例に見方を見てみます。まず1.96=1.9+0.06とわけます。そして、1.9と0.06が交差するところを調べます。そうすると、0.4750とわかります。つまり0〜1.96の範囲では0.4750の面積を占めるわけです。0.4750×2=0.95ですから、冒頭の−1.96〜1.96の範囲では面積0.95占めるという話と当然一致します。

 

 

このように標準正規分布表を使うことができます。

 

 

面積と確率

もうここまで理解している方であれば、確率密度関数のグラフとある横軸の値で囲まれる面積は確率と等しくなるということがわかってきたのではないかと思います。少し例を交えてみていきます。

 

薬理のテストをしたところ、平均点が60点で標準偏差が20の正規分布だったとしましょう。

 

 

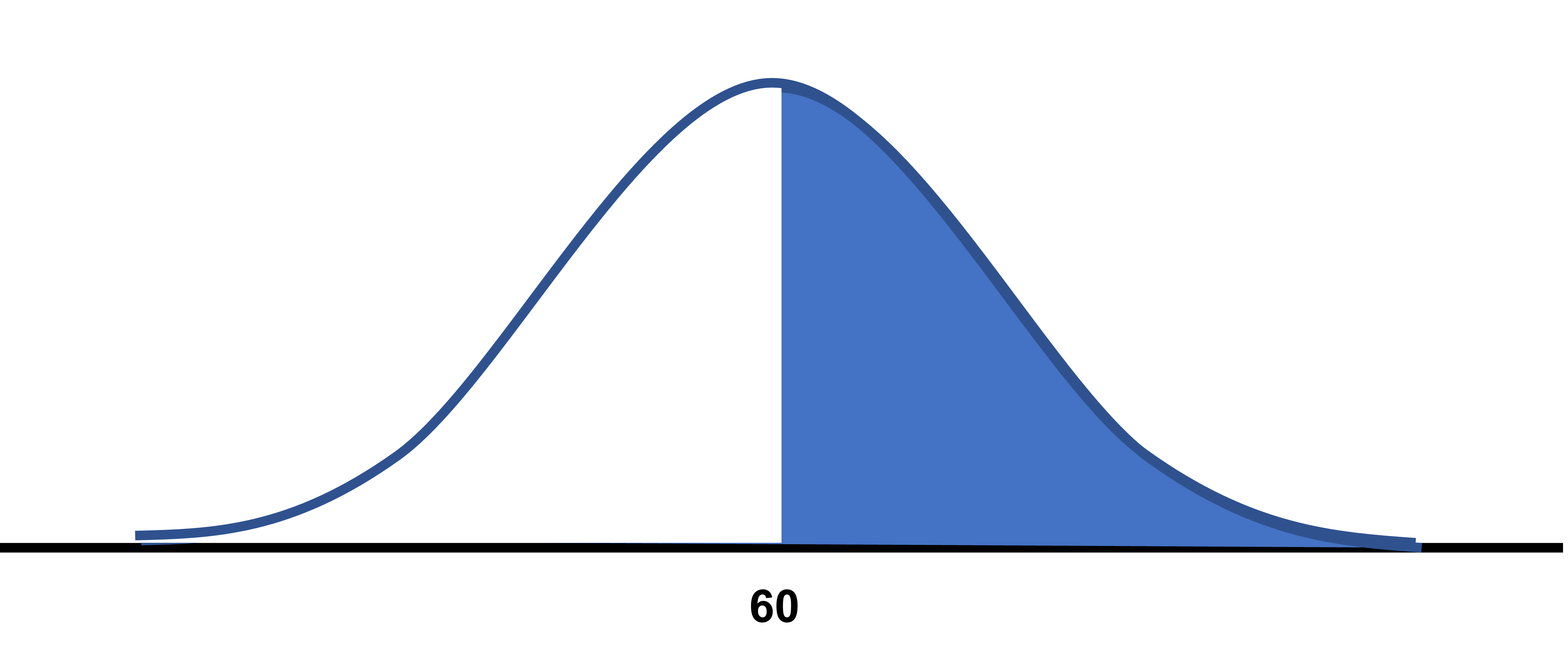
この時グラフを見ると、60点から右側の面積は0.5であることはわかると思います。そして60点以上の人は、平均点から右側にいるので50%を占めるのもわかると思います。このことからわかるように標準正規分布などの確率密度関数のグラフとある横軸の値で囲まれる面積と確率が等しくなることがわかりますね。

 

まとめ

• 確率密度関数のグラフと横軸で囲まれる面積は1となる
• 標準正規分布表は、横軸の値と確率密度関数のグラフで囲まれる面積がどれくらい占めているのかを表している
• 確率密度関数のグラフとある横軸の値で囲まれる面積は確率と等しくなるということができる