Sponsored Link
クラメールの連関係数と例題
前回の相関比の求め方と例題では相関比を見ました。今回はクラメールの連関係数を見てみます。
クラメールの連関係数とは
相関比は、数量データとカテゴリーデータの組み合わせでした。今回見るクラメールの連関係数はカテゴリーデータとカテゴリーの組み合わせにおける指標を言います。早速例題を見てみましょう。
薬学部の男性と女性を集めて衛生と薬剤どちらの科目が好きかを質問したところ、以下の結果が得られた。この時のクラメールの連関係数を求めよ。
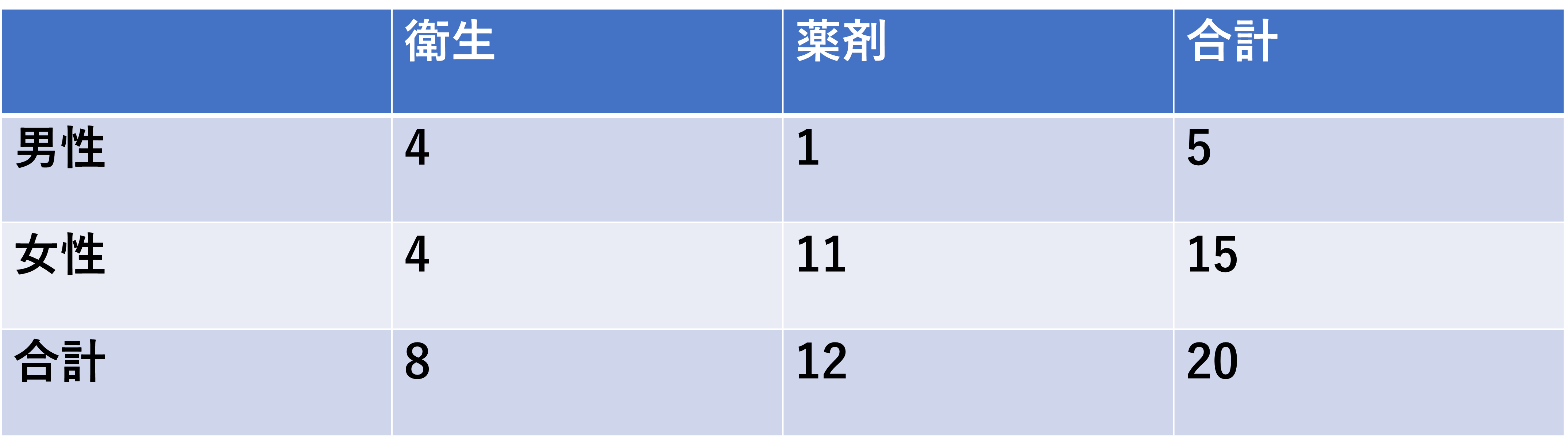
クラメールの連関係数は以下の手順で求めます。
- 実測度数を求める
- 期待度数を求める
- ピアソンのカイ二乗統計量を求める
- クラメールの連関係数を求める。
Sponsored Link
Sponsored Link
実測度数を求める
先ほどの図における赤字の値は実測度数と言います。
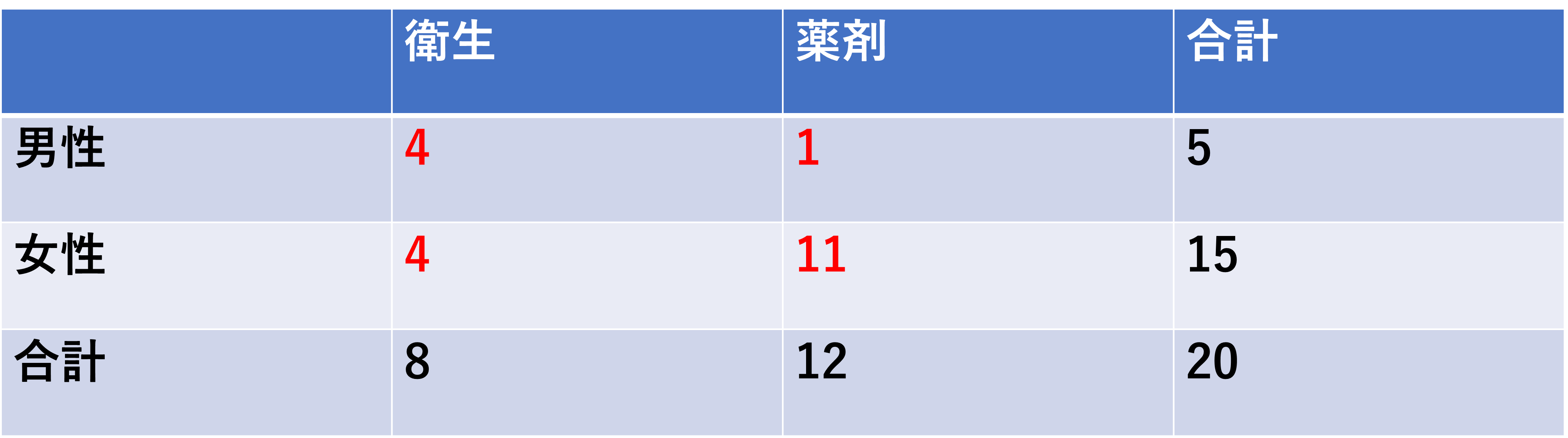
期待度数を求める
先ほど確認した実測度数をもとに、各カテゴリーデータの合計値に各カテゴリーデータをかけて、それを全体数で割ったものを期待度数と言います。図でいうところの緑色が期待度数です。
例えば男性で衛生のところであれば、男性の合計値は5、衛生の好きな人の合計値は8なので、それを全体数20で割った5×8÷20となります。
これを各項目埋めたものが緑色のものになります。
ピアソンのカイ二乗統計量を求める
先ほど確認した実測度数と期待度数をもとに、それぞれのマスに(実測度数−期待度数)^2/期待度数を行います。図でいうところのオレンジの値になるはずです。
そして、それらを足し合わせたものがピアソンのカイ二乗統計量となります。
ピアソンのカイ二乗統計量=2.00+1.33+0.67+0.44=4.44
クラメールの連関係数を求める。
クラメールの連関係数は
- √｛ピアソンのカイ二乗統計量/(全データ数×カテゴリーデータの項目のうち少ない方−1)
で求められます。ピアソンのカイ二乗統計量は4.44、全データ数は20となります。問題は「カテゴリーデータの項目のうち少ない方−1」です。今回、性別と科目というカテゴリーデータを扱いました。性別は男性と女性の2つ、科目は衛生と薬剤の2つということでどちらも項目的には2なので、今回カテゴリーデータの項目のうち少ない方は2となります。ここから1を引くことになるので、1となります。
一応カテゴリーデータの項目のうち少ない方の補足として、性別の項目は変わらず男性と女性の2つのまま、科目は薬理を加えたとしたら、衛生、薬剤、薬理とすると3つになります。この場合は性別の項目の方が2と少ないのでこちらが選ばれて2とするということです。そして同様に1を引くので1となります。
以上よりクラメールの連関係数を求めると、
√｛4.44/(20×1)=0.471
これが答えです。
クラメールの連関係数も、相関比と同じく0〜1の間の数字となり、マイナスは出てきません。√｛ピアソンのカイ二乗統計量/(全データ数×カテゴリーデータの項目のうち少ない方−1)という式からもわかるようにマイナスになる要素がないからです。そして、毎度のようにいくつで関連しているという基準はないので、参考程度にみると
0.8〜1；非常に強い関連
0.5〜0.8；やや強い関連
0.25〜0.5；やや弱い関連
0〜0.25；非常に弱い関連(無関係)
これより今回はやや弱い関連となります。
まとめ
- カテゴリーデータとカテゴリーデータの関連性の指標として、クラメールの連関係数がある。
就職や転職でお悩みの方はコチラ！私はここで年収120万円上がりました
Sponsored Link
クラメールの連関係数と例題 関連ページ
- 母集団と標本
- 統計学とは、簡単に言うと標本の情報から母集団の状況を推測する学問です。母集団とは本来調査するべき全員を指し、その一部を標本ということができます。
- 数量データとカテゴリーデータ
- 統計学では、目盛が等間隔で測れるデータを数量データと言います。目盛が等間隔ではなく測れないものをカテゴリーデータと言います。
- カテゴリーデータと単純集計表
- カテゴリーデータをまとめたものは単純集計表と呼ばれることがあります。単純集計表の作り方は、カテゴリーデータの各項目を数えて、割合を出すことで作られます。
- 度数分布表の作り方、基礎編
- データから度数分布表の作り方は、最大値と最小値を把握する、階級を決める、階級値を決める、度数を数える、相対度数を出すというように行います。
- ヒストグラムの作り方、基礎編
- ヒストグラムとはいわゆる棒グラフのことで、横軸は階級値、縦軸は度数(相対度数)などにより描かれます。度数分布表やヒストグラムを作ることで、より直感的にデータの特徴を感じることができます
- 度数分布表とヒストグラム、例題編
- 今まで見てきた度数分布表とヒストグラムの作り方をもとに、例題を交えてさらに理解できるようにします。度数分布表とヒストグラムを慣れるまで繰り返しましょう。
- 平均値と中央値の違い
- 平均値とはデータの合計値を全データで割ったもので、中央値はデータを小さい順から並べたときに真ん中にくるものです。そのため平均値と中央値は違います。
- 分散とは？
- 平均値のみではデータの散らばりの判断がつかないので、分散を知る必要があります。分散は偏差の二乗の合計値を全データで割って求めることができます。
- 標準偏差、基礎編
- 分散の欠点を解消するために√をとったものが標準偏差であり統計学ではかなり重要です。標準偏差は0であればデータが全く散らばっていなく、大きくなるほど散らばっていることを示しています。
- 標準偏差、例題編
- 標準偏差の求め方は、平均値を出す、偏差を出す、分散を出す、標準偏差を出すという手順で出すことができます。薬学部において標準偏差を出すことができればかなりの進歩です。
- 統計学で偏差値を考える
- CBTや国家試験の模試を行うと、偏差値が出てきます。統計学の平均値や標準偏差の知識を用いることで、テストの偏差値や1点の重みがわかります。
- 基準値と偏差値
- 偏差値は基準値×10+50で出すことができます。偏差値は基準値をもとにして出されるので、満点の点数が違うものや、単位が違うものも比較できます。
- 標準偏差を用いて、データの特殊性を評価する
- 標準偏差1個以内にあるものは全体の70%を占め、月並みなデータですが、2個以上離れているデータは正規分布する場合前回の5%しか存在せず、かなり特殊なデータと言える。
- データに一定数を加えた時の平均値や標準偏差への影響
- データに一定数を加えて加工すると平均値のみ変化して標準偏差には影響を与えません。これはヒストグラムがただ横にスライドするだけと考えるとわかりやすいでしょう。
- データに一定数をかけた時の平均値や標準偏差への影響
- データに一定数をかけた場合、平均値も標準偏差もかけた数だけ増えます。つまり没問が出た場合、標準偏差にも影響が出てしまうため得点を二倍にしてはいけません。
- 正規分布の式とグラフ
- ヒストグラムの階級を限りなく狭めていくと曲線になっていき、その曲線の式を確率密度関数といいます。正規分布は確率密度関数の1つで左右対称の山のようなグラフとなります。
- 標準正規分布と性質
- 平均が0で標準偏差が1の時は、xは標準正規分布に従います。正規分布の特性としてμ±σの範囲のデータの相対度数は約70%がこの中に入り、μ±2σの範囲のデータの相対度数は約95%がこの中に入ります。
- 標準正規分布の95%予言的中区間
- 標準正規分布は無限の数字をとる可能性がありますが、その性質を利用することで次に出てくるデータを推測することができます。標準正規分布の95%予言的中区間は−1.96〜＋1.96です。
- 正規分布の95%予言的中区間と例題
- 標準正規分布のデータに一定数σをかけて、さらに一定数μを足して加工するため、正規分布の95%予言的中区間は、μ−1.96σ〜μ+1.96σです。
- 標準正規分布表、面積と確率
- 標準正規分布表は、横軸の値と確率密度関数のグラフで囲まれる面積がどれくらい占めているのかを表しています。またこの面積は確率と等しくなります。
- データから母集団を推定する方法
- 正規分布の95%予言的中区間を使うことで、データから母集団を推定することができます。この時に、仮説が妥当ではない場合は仮説を棄却すると統計学では言います。
- 95%信頼区間とは
- 95%信頼区間とは様々な観測値から同じ方法で区間推定をして、そのうち95%は正しい母数を含んでいるものを言います。−1.96≦(N−μ)/σ≦+1.96で95%信頼区間は求めます
- 無作為抽出の仮定と母平均
- 無作為抽出の仮定を用いると、階級値×相対度数の合計=平均値をあてはめることができ、ここから出した平均値を母平均といいます。
- 母標準偏差の出し方
- 度数分布表から母分散を出す場合、(偏差の二乗×相対度数)の合計で出す必要があります。また母分散に√(ルート)をとったものが母標準偏差です。
- 標本平均とは
- 1つの母集団からn個のデータを観測して標本平均を作ると、nが大きいほど標本平均は母平均に近い数値をとる可能性が高くなります。
- 正規分布している母集団からの標本平均における95%予言的中区間
- 母集団が正規分布している場合は、そこから標本平均を作った場合も正規分布します。正規分布している母集団からの標本平均における95%予言的中区間はμ−1.96σ/√n〜μ+1.96σ/√nです。
- 標本平均から母集団の母平均を推定する
- 観測データから母集団の母平均μを推測する場合は、95$信頼区間を利用して、標本平均が予言の範囲に入るような母平均を持つ母集団のみ妥当なものとして残す
- 標本分散の性質
- 標本分散=｛(偏差1)^2+(偏差2)^2+・・・・+(偏差n)^2｝/nで表されます。分子も分母も必ずプラスになるため、標本分散は必ずプラスとなり正規分布しなくなります。
- カイ二乗分布とは？自由度とヒストグラム
- 標本分散はカイ二乗分布となり自由度は、標本数を表します。カイ二乗分布のヒストグラムは自由度によって形が変化していきます。
- カイ二乗分布表の読み方と例題
- カイ二乗分布表は標準正規分布表とは異なり、横軸以上の面積が占める割合を表しています。カイ二乗分布表の読み方と例題をまとめてみました。
- 母分散をカイ二乗分布で推定する方法
- (標本−母平均)/母標準偏差を行うことで、標準正規分布に変換できます。つまりこの変換を行いカイ二乗分布をとることで、95%予言的中区間を利用することができます。
- (標本−標本平均)/母標準偏差の二乗の和はカイ二乗分布する
- (標本−標本平均)/母標準偏差の二乗の和は標本分散に比例するためカイ二乗分布をとります。ただし、自由度がn−1となります。
- (標本−標本平均)/母標準偏差の二乗の和の自由度が1下がる理由
- (標本−標本平均)/母標準偏差の二乗の和は元は2つだったデータが式変形することで1つに減るため、自由度が1下がったカイ二乗分布となります。
- 母平均が未知の正規母集団の区間推定の例題
- (標本−標本平均)/母標準偏差の二乗の和を出すことで母平均が未知の正規母集団を区間推定することが可能となります。それの例題となります。
- t分布と統計量Tとは？
- 統計量Tを出して、t分布がわかれば、未知の母平均を推定することができます。統計量T=(標本平均−母平均)×√(n−1)/標本標準偏差で求められます。
- t分布のヒストグラムと統計量Tの計算例題
- t分布のヒストグラムは正規分布に似たような山のようなグラフを描きます。t分布と正規分布の違いは、山のてっぺんと山の麓の高さが違います。
- t分布表の読み方
- t分布表の確率95%の数字を見て、そのプラスマイナスで挟まれる範囲の面積が95%となります。t分布は自由度が上がるにつれて正規分布に近づいていくため、自由度が∞の時の確率95%は標準正規分布と一緒の1.96となります。
- t分布を利用した未知の母平均の区間推定、例題
- 統計量Tとt分布表を用いることで、未知の母平均を推定することができます。薬学部の統計学ではt分布までできていれば、かなりのレベルまで達しています。
- 相関分析、単相関係数と例題
- 相関分析のうち、数量データと数量データの組み合わせにおける指標を単相関係数といいます。単相関係数の求め方を例題とともにまとめました。
- 正の相関と負の相関
- 単相関係数の値がプラスの場合は正の相関がある、マイナスの場合は負の相関があると言います。単相関係数が0に近い場合は、2変数が関連していないことを意味します。
- 相関比の求め方と例題
- 数量データとカテゴリーデータの関連性の指標として、相関比があります。相関比=級内変動/(級内変動+級間変動)で求めることができます。求め方と例題をまとめました。