確率分布の特徴

前回のヒストグラムの作り方、基礎編までで統計学をやるうえで重要となる分布についてみてきました。統計学をやるうえで大事なことがもう1つあります。それが確率です。度数分布表を学んだ時に軽く触れていますが、改めて今回は確率についてみていきたいと思います。

 

 

確率とは

分布に対して確率は普段から皆さんがよく使っている言葉だと思います。「統計学意味不明だし、勉強してないから、明日の統計学のテストは99%落ちる」といった感じで使っていると思います(笑)冗談はさておき、改めて確率とは何なのでしょうか？

 

確率の「確」は確からしさ、「率」は割合を意味していて、確率とは「ある現象が起こる確かさを割合で表したもの」ということができます。

 

先ほどは99%というようにパーセント(%)を用いましたが、統計学で確率を使う場合はパーセントは使わずに割合を使います。薬学部に入っている皆さんはさすがに大丈夫かと思いますが、さきほどの99%を割合で表すと、0.99となりますね。その他、2.5%であれば0.025となります。

 

 

確率分布

確率の基本を確認したところで、前回までの分布と今回の確率を合体させた確率分布についてみてみます。前回やった身長のヒストグラムや度数分布表を改めてみてみましょう。

 

 

 

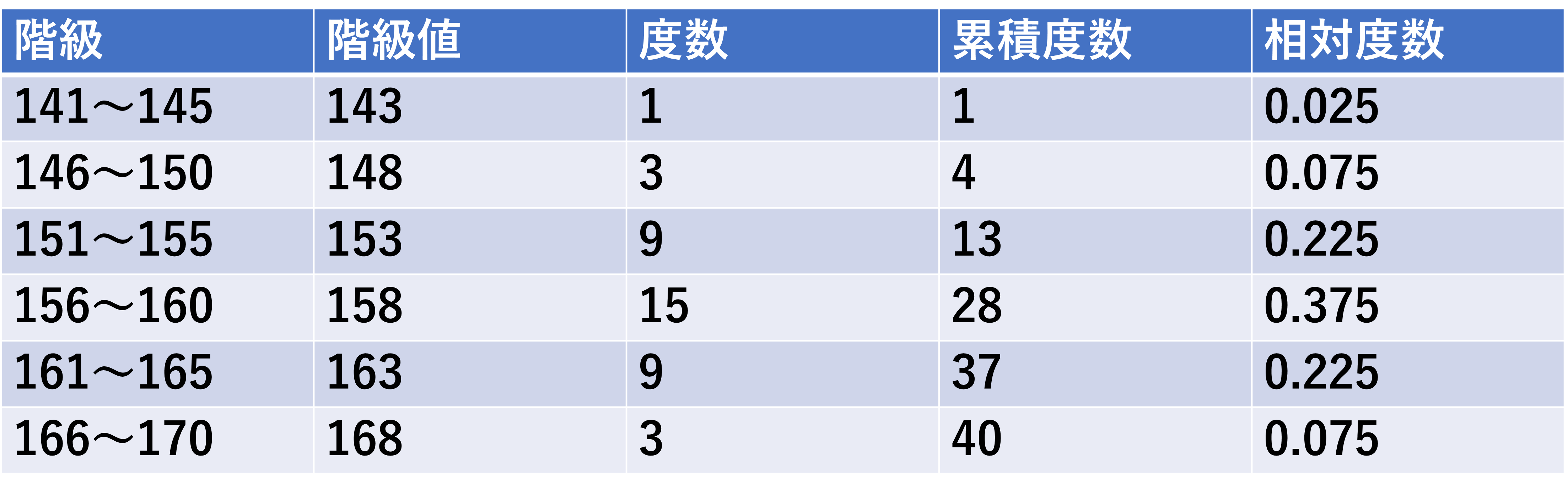
ヒストグラムの一番右の柱は「身長166〜170cmの相対度数が0.075」ということを表しています。このことを確率に置き換えると、「身長が166〜170である確率は0.075」ということを表しています。皆さんになじみのある%で言うと、「身長が166〜170である確率は7.5%」とも言えます。これを全ての階級で言うと

 

• 身長が141〜145である確率は0.025
• 身長が146〜150である確率は0.075
• 身長が151〜155である確率は0.225
• 身長が156〜160である確率は0.375
• 身長が161〜165である確率は0.225
• 身長が166〜170である確率は0.075

 

となります。今回は身長についてみてみましたが、身長以外にも身の回りの様々なものが確率分布します。

 

確率分布の特徴

度数分布表のページで簡単に確認済みではありますが、確率分布は以下の特徴を持ちます。

 

• 確率分布のそれぞれの確率は、0〜1の間の値をとる
• 確率は最も小さい時で0であり、マイナスにはならない
• 確率は最も大きい時は1であり、1を超えることはない
• 確率分布のそれぞれの確率を全て足すと、必ず1になる

 

相対度数は、各度数を全データで割ったものであることを考えれば、この特徴はすんなりと受け入れてもらえると思います。念のための確認でした。

 

まとめ

• 確率分布のそれぞれの確率を全て足すと、必ず1になる