Sponsored Link
度数分布表の作り方、基礎編
前回のカテゴリーデータと単純集計表では、カテゴリーデータについて見ました。今回は数量データについてもう少し深掘りし、度数分布表について見ていきたいと思います。
度数分布表
前回では、当サイトについてアンケートをとった例についてお話ししました。そのアンケートの項目に私が皆様に「身長はどれくらいですか？」と質問したところ以下のようなデータが得られたとしましょう。
この数字を見て何かわかることはあるでしょうか？
おそらく私を含めて多くの人は、「数字があるなぁ」くらいにしか思わないと思います(笑)そして実際に様々な身長の数字をとっていることくらいはわかります。この様々な数字をとることを統計学では分布すると言います。
この分布している数字ですが、なんらかの特徴をもって分布していますが、先ほどもお話ししたように普通の人であればただの数字にしか見えません。そこで統計学では分布の特徴を見出すために整理整頓をしていき、意味のあるデータだけを抽出していきます。
整理整頓して直感的にわかりやすくするにはグラフ化するのがわかりやすいですね。そのため、グラフ化するために以下の手順で準備を行います。
- 最大値と最小値を把握する
- 階級を決める
- 階級値を決める
- 度数を数える
- 相対度数を出す
Sponsored Link
Sponsored Link
最大値と最小値を把握する
まず各身長について区切りをつけていきます。数字を見たときに一番大きい身長は170、一番小さい身長は141です。全ての身長はこの範囲に収まることがわかります。
階級を決める
次に141〜170が収まるよう、区切りのいい5cmきざみで分類していきます。つまり
- 141〜145
- 146〜150
- 151〜155
- 156〜160
- 161〜165
- 166〜170
このようにわけます。この区切りを統計学では階級と言います。
階級値を決める
先ほど階級を作りましたが、その真ん中の値を階級値と呼びます。166、167、168、169、170では真ん中の数字は168となります。これを全ての階級で行うと
- 141〜145；階級値143
- 146〜150；階級値148
- 151〜155；階級値153
- 156〜160；階級値158
- 161〜165；階級値163
- 166〜170；階級値168
となります。
度数を数える
各階級にあるデータの数を度数と言います。166〜170では、3個この中に当てはまる数字があるので、度数は3となります。これを全ての階級で行うと
- 141〜145；階級値143；度数1；累積度数1
- 146〜150；階級値148；度数3；累積度数4
- 151〜155；階級値153；度数9；累積度数13
- 156〜160；階級値158；度数15；累積度数28
- 161〜165；階級値163；度数9；累積度数37
- 166〜170；階級値168；度数3；累積度数40
となります。
この度数を上から数えたものを累積度数と言い、最後の166〜170までやると当然全データの40となります。
度数を数えることで、今回のデータは156〜160に身長が集まっていることがわかりますね。
相対度数を出す
各度数を全データで割ったものを相対度数と言います。166〜170では、度数が3ありました。全データ数は40なので、これで割ると3÷40=0.075となります。これを全ての階級で行うと
- 141〜145；階級値143；度数1；累積度数1；相対度数0.025
- 146〜150；階級値148；度数3；累積度数4；相対度数0.075
- 151〜155；階級値153；度数9；累積度数13；相対度数0.225
- 156〜160；階級値158；度数15；累積度数28；相対度数0.375
- 161〜165；階級値163；度数9；累積度数37；相対度数0.225
- 166〜170；階級値168；度数3；累積度数40；相対度数0.075
となります。
相対度数を出すことで、それぞれの度数が何%占めているかわかります。例えば、156〜160では先ほどざっくりと数が多いことは度数からわかりましたが、相対度数が0.375なので、37.5%占めていることがわかります。
補足ですが統計のテストの時には、間違い確認として、相対度数の合計値が1となることを念のため確認しておきましょう。
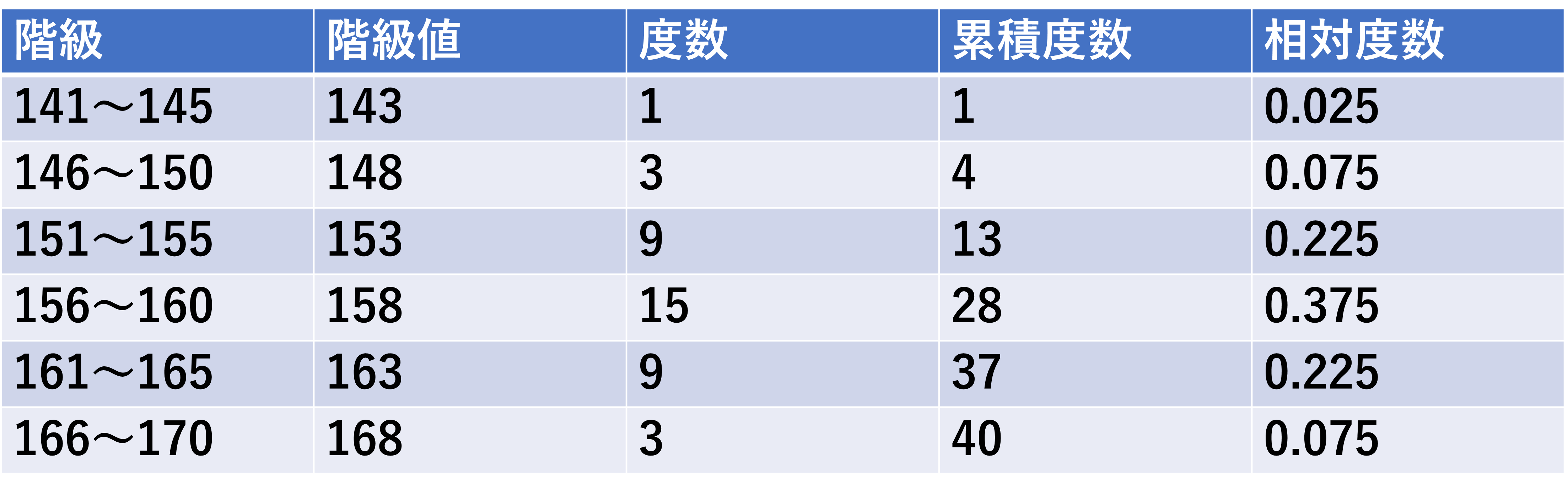
このようにして、まとめたものを度数分布表と言います。度数分布表を作ることで、元の40個がどのようなデータであったかがわからなくなってしまいますが、代わりに始めにわからなかった分布の特徴を見ることができます。
例えば、すでに説明済みですが、156〜160にデータが集まっている。また156〜160を起点にして身長が低い方にも高い方にも左右対称にデータが分布している。などが度数分布表から読み取れます。
つまり今回のはじめのデータから度数分布表にする作業を会話に置き換えると、はじめの40個のデータは会話の全てとなります。それに対して、度数分布表は会話のまとめということができます。
まとめ
- データから度数分布表の作り方は、最大値と最小値を把握する、階級を決める、階級値を決める、度数を数える、相対度数を出すというように行う。
- 度数分布表を作ることで、元のデータは失われるが、データの特徴を見出すことができる。
就職や転職でお悩みの方はコチラ！私はここで年収120万円上がりました
Sponsored Link
度数分布表の作り方、基礎編 関連ページ
- 母集団と標本
- 統計学とは、簡単に言うと標本の情報から母集団の状況を推測する学問です。母集団とは本来調査するべき全員を指し、その一部を標本ということができます。
- 数量データとカテゴリーデータ
- 統計学では、目盛が等間隔で測れるデータを数量データと言います。目盛が等間隔ではなく測れないものをカテゴリーデータと言います。
- カテゴリーデータと単純集計表
- カテゴリーデータをまとめたものは単純集計表と呼ばれることがあります。単純集計表の作り方は、カテゴリーデータの各項目を数えて、割合を出すことで作られます。
- ヒストグラムの作り方、基礎編
- ヒストグラムとはいわゆる棒グラフのことで、横軸は階級値、縦軸は度数(相対度数)などにより描かれます。度数分布表やヒストグラムを作ることで、より直感的にデータの特徴を感じることができます
- 度数分布表とヒストグラム、例題編
- 今まで見てきた度数分布表とヒストグラムの作り方をもとに、例題を交えてさらに理解できるようにします。度数分布表とヒストグラムを慣れるまで繰り返しましょう。
- 平均値と中央値の違い
- 平均値とはデータの合計値を全データで割ったもので、中央値はデータを小さい順から並べたときに真ん中にくるものです。そのため平均値と中央値は違います。
- 分散とは？
- 平均値のみではデータの散らばりの判断がつかないので、分散を知る必要があります。分散は偏差の二乗の合計値を全データで割って求めることができます。
- 標準偏差、基礎編
- 分散の欠点を解消するために√をとったものが標準偏差であり統計学ではかなり重要です。標準偏差は0であればデータが全く散らばっていなく、大きくなるほど散らばっていることを示しています。
- 標準偏差、例題編
- 標準偏差の求め方は、平均値を出す、偏差を出す、分散を出す、標準偏差を出すという手順で出すことができます。薬学部において標準偏差を出すことができればかなりの進歩です。