Sponsored Link
数量データとカテゴリーデータ
前回の母集団と標本では、統計学はどういう学問なのかを母集団と標本という単語を交えて話しました。今回は統計学に使われるデータについて見ていきたいと思います。
測れるデータと測れないデータ
統計学はどうしても数字のイメージが強いですが、その他にも様々なデータが使われます。その様々なデータには測れるものと測れないものが存在します。例えば、当サイトについて以下のようなアンケートを皆様にとったとします。
当サイトはわかりやすいか？
- とてもわかりやすい
- ややわかりやすい
- どちらともいえない
- ややわかりにくい
- とてもわかりにくい
あなたは薬学部何年生ですか？
- ○○年生
あなたの性別は？
- 男
- 女
当サイトを1週間にどれくらい見ますか？
- ○○回
このアンケートについて以下のような回答が得られたとします。
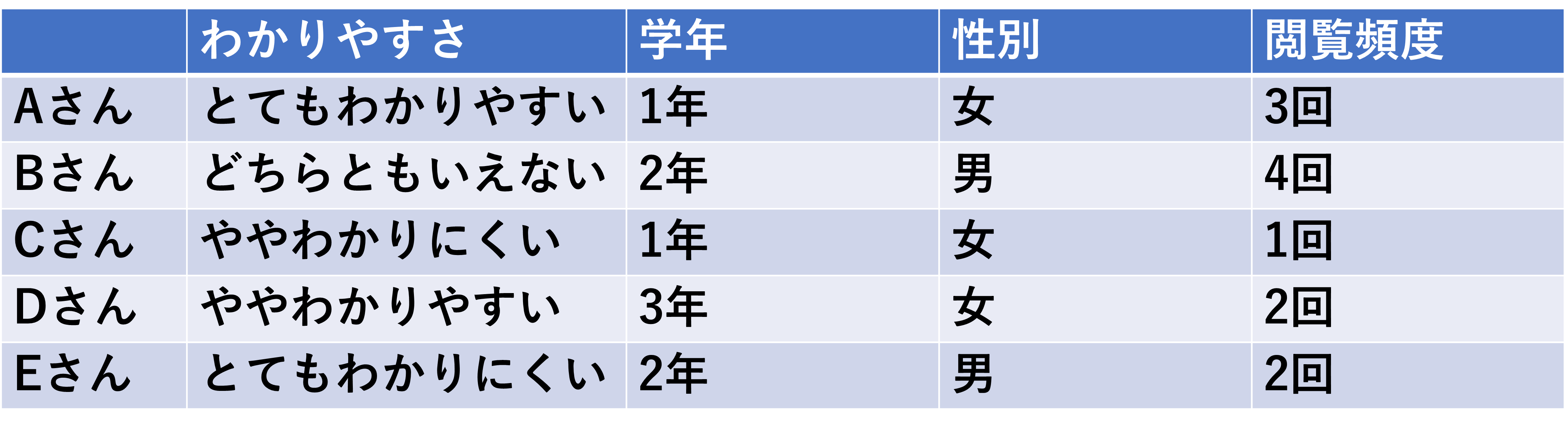
では、このアンケートの回答結果ですが、測れるデータと測れないデータがあるのですがわかるでしょうか？先ほどのアンケートについては以下のように分類できます。
- 測れるデータ；あなたは薬学部何年生ですか？、当サイトを1週間にどれくらい見ますか？
- 測れないデータ；当サイトはわかりやすいか？、あなたの性別は？
測れるデータというのは、目盛が等間隔であるため測ることができます。それに対して測れないデータは、目盛が等間隔ではありません。特に最初の当サイトはわかりやすいか？というのは個人の尺度で決まっているものなので、それぞれのわかりやすさの間隔は等しいと言えないから測れないわけです。
測れるデータのことを数量データ、測れないデータのことをカテゴリーデータと呼びます。
ちなみに本当にtwitterでたまに皆様にアンケートをとっていますが、その時に当サイトを「とてもわかりやすい」とアンケートに答えてくれるのを楽しみにしています(笑)
では、例題と共にもう少し数量データとカテゴリーデータをみてみましょう。
Sponsored Link
Sponsored Link
例題
ある開発中の高血圧治療薬をAさんに治験で投与し、以下のデータ得られた。このデータについて数量データとカテゴリーデータで分類せよ
- 年齢；20歳
- 血液型；B型
- 職業；大学生
- 治験薬投与1時間後の血圧；120
- 治験薬投与1時間後の脈拍；80
- 治験薬投与1時間後の体温；37
- 治験薬投与1時間後の呼吸数；20
- 治験薬の味についての評価；苦かった
年齢、血圧、脈拍、体温、呼吸数は、目盛が等間隔のため数量データとなります。血液型、職業、味の評価については目盛が等間隔ではないのでカテゴリーデータとなります。
まとめ
- 目盛が等間隔で測れるデータを数量データと言う。目盛が等間隔ではなく測れないものをカテゴリーデータと言う。
就職や転職でお悩みの方はコチラ！私はここで年収120万円上がりました
Sponsored Link
数量データとカテゴリーデータ 関連ページ
- 母集団と標本
- 統計学とは、簡単に言うと標本の情報から母集団の状況を推測する学問です。母集団とは本来調査するべき全員を指し、その一部を標本ということができます。
- カテゴリーデータと単純集計表
- カテゴリーデータをまとめたものは単純集計表と呼ばれることがあります。単純集計表の作り方は、カテゴリーデータの各項目を数えて、割合を出すことで作られます。
- 度数分布表の作り方、基礎編
- データから度数分布表の作り方は、最大値と最小値を把握する、階級を決める、階級値を決める、度数を数える、相対度数を出すというように行います。
- ヒストグラムの作り方、基礎編
- ヒストグラムとはいわゆる棒グラフのことで、横軸は階級値、縦軸は度数(相対度数)などにより描かれます。度数分布表やヒストグラムを作ることで、より直感的にデータの特徴を感じることができます
- 度数分布表とヒストグラム、例題編
- 今まで見てきた度数分布表とヒストグラムの作り方をもとに、例題を交えてさらに理解できるようにします。度数分布表とヒストグラムを慣れるまで繰り返しましょう。
- 平均値と中央値の違い
- 平均値とはデータの合計値を全データで割ったもので、中央値はデータを小さい順から並べたときに真ん中にくるものです。そのため平均値と中央値は違います。
- 分散とは？
- 平均値のみではデータの散らばりの判断がつかないので、分散を知る必要があります。分散は偏差の二乗の合計値を全データで割って求めることができます。
- 標準偏差、基礎編
- 分散の欠点を解消するために√をとったものが標準偏差であり統計学ではかなり重要です。標準偏差は0であればデータが全く散らばっていなく、大きくなるほど散らばっていることを示しています。
- 標準偏差、例題編
- 標準偏差の求め方は、平均値を出す、偏差を出す、分散を出す、標準偏差を出すという手順で出すことができます。薬学部において標準偏差を出すことができればかなりの進歩です。
- 統計学で偏差値を考える
- CBTや国家試験の模試を行うと、偏差値が出てきます。統計学の平均値や標準偏差の知識を用いることで、テストの偏差値や1点の重みがわかります。
- 基準値と偏差値
- 偏差値は基準値×10+50で出すことができます。偏差値は基準値をもとにして出されるので、満点の点数が違うものや、単位が違うものも比較できます。
- 標準偏差を用いて、データの特殊性を評価する
- 標準偏差1個以内にあるものは全体の70%を占め、月並みなデータですが、2個以上離れているデータは正規分布する場合前回の5%しか存在せず、かなり特殊なデータと言える。