独立性の検定におけるExcelを用いたP値の求め方

前回の独立性の検定の計算、例題では独立性の検定を見ました。独立性の検定では、検定統計量が棄却域に入っているかどうかで判断していましたが、もう1つ判断する方法があります。それがP値と呼ばれるもので、今回は独立性の検定におけるP値についてみていきたいと思います。

 

 

独立性の検定におけるP値とは

前回の例題では、優位水準0.05は3.841以上の領域を指していました。独立性の検定におけるP値とは、そこの確率のことを指しています。そして、優位水準よりもP値が小さいかどうかで判断します。

 

いつものように、これだけみても意味不明だと思うので、早速例題です。

 

 

例題

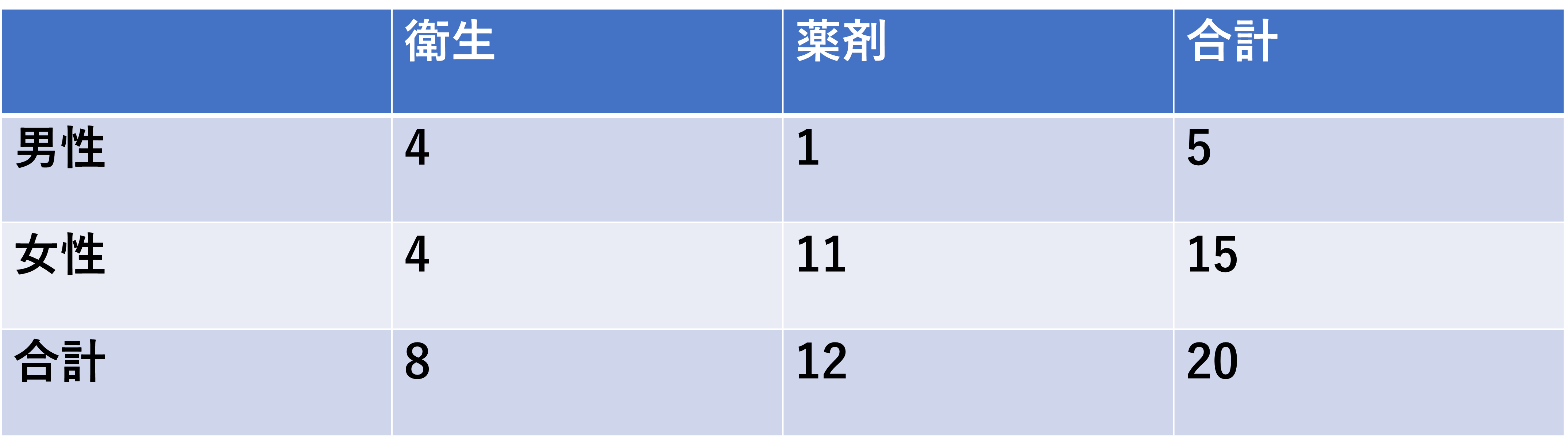
某薬学部の学生からランダムに20人を選び衛生か薬剤どちらの科目が好きかをアンケートして以下の結果が得られた。母集団の某薬学部における性別と好きな科目は関連しているかどうかをP値を用いて独立性の検定により推測せよ。ただし優位水準は0.05とする。

 

 

独立性の検定におけるP値は以下のような手順で行います。途中までは前回と同じなので、割愛して肝となるP値の求め方を解説していきます。

 

1. 母集団を定義する
2. 帰無仮説と対立仮説を決める
3. 行う検定を選ぶ
4. 優位水準を決める
5. 標本データからP値を求める
6. 求めたP値が優位水準よりも小さいかを確認し結論を出す。

 

途中までは前回と同じなので、割愛して肝となる標本データからP値の求めるから解説していきます。

 

標本データからP値を求める

P値の計算はパソコンが出てくるまでは大変だったので、前回までの検定統計量が棄却域に入っているかどうかで結論を下さしていました。ただ文明の利器Excelが出てきて簡単に求められるようになったので、Excelを用いたP値の出し方を見てみます。先に結論として以下の表の作成を目指します。

 

 

Excelを起動して、まずそれぞれのセルに以下の項目を打ちます。

 

• A2；男性
• A3；女性
• A4；合計
• B1；衛生
• B2；4
• B4；8
• C1；薬剤
• C2；1
• C3；11
• C4；12
• D1；合計
• D2；5
• D3；15
• D4；20

 

これでとりあえず、問題文のデータが打てたと思います。次に以下の項目を打ちます。

 

• A7；男性
• A8；女性
• B6；衛生
• C6；薬剤

 

次にB7に、「=D2*B4/D4」と打ち、D2を選択してF4キーを3回押し、D2が$D2になったことを確認します。さらに、D4を選択してF4キーを1回押して、$D$4となっていることを確認してEnterキーを押します。

 

B7のセルを選択して、マウスの先端をB7セルの右下角に合わせると、マウスのポインタが矢印から黒十字になるので、マウスの左を押しながらC7まで引っ張り左ボタンを離す。

 

この作業をB8セルも同じように行うと$D2*C4/$D$4となるはずです。そして、同様に引っ張りC8セルも埋めます。

 

最後にA10にP値と打ち、B10を選択して、メニューバーの「数式」などから「関数の挿入」を選び、関数名で「CHITEST」を選びます。

 

実測値範囲にB2:C3と打ち、期待値範囲にB7:C8と打ち、OKボタンを押すとP値が出てきます。今回の場合は0.035015となるはずです。

 

求めたP値が優位水準よりも小さいかを確認し結論を出す。

優位水準よりもP値が小さければ対立仮説は正しいとして、そうでなければ帰無仮説は誤っているとは言えないとします。

 

先ほど出したP値が0.035015と0.05より小さいです。よって、対立仮説は正しいとします。

 

まとめ

• Excelを用いることで、独立性の検定におけるP値を簡単に求めることができる。