正の相関と負の相関

前回の相関分析、単相関係数と例題では単相関係数についてみました。今回は正の相関や負の相関についてみていきたいと思います。

 

 

正の相関と負の相関

前回の例題で単相関係数は最終的に0.844という値が得られました。単相関係数は−1〜＋1までの値をとり、2変数が関連しているほど±1に近づきます。よって0.844という数字は1に結構近いので年齢が血圧に関連しているというのが、グラフ以外でもわかります。

 

今回の年齢と血圧の例のように、単相関係数の値がプラスの場合は正の相関があると言います。一般的に正の相関と考えられている他の例としては、タバコの本数と肺がんの発生率などがあります。

 

では逆に単相関係数が−1に近い数字が出てきたらどう考えればよいでしょうか？

 

それは年齢が高いほど血圧が下がっていくことを意味しています。なかなか現実的にはありえないですが、前回確認したグラフが右肩下がりのグラフになります。説明用として、グラフの数値を少しいじりました。

 

 

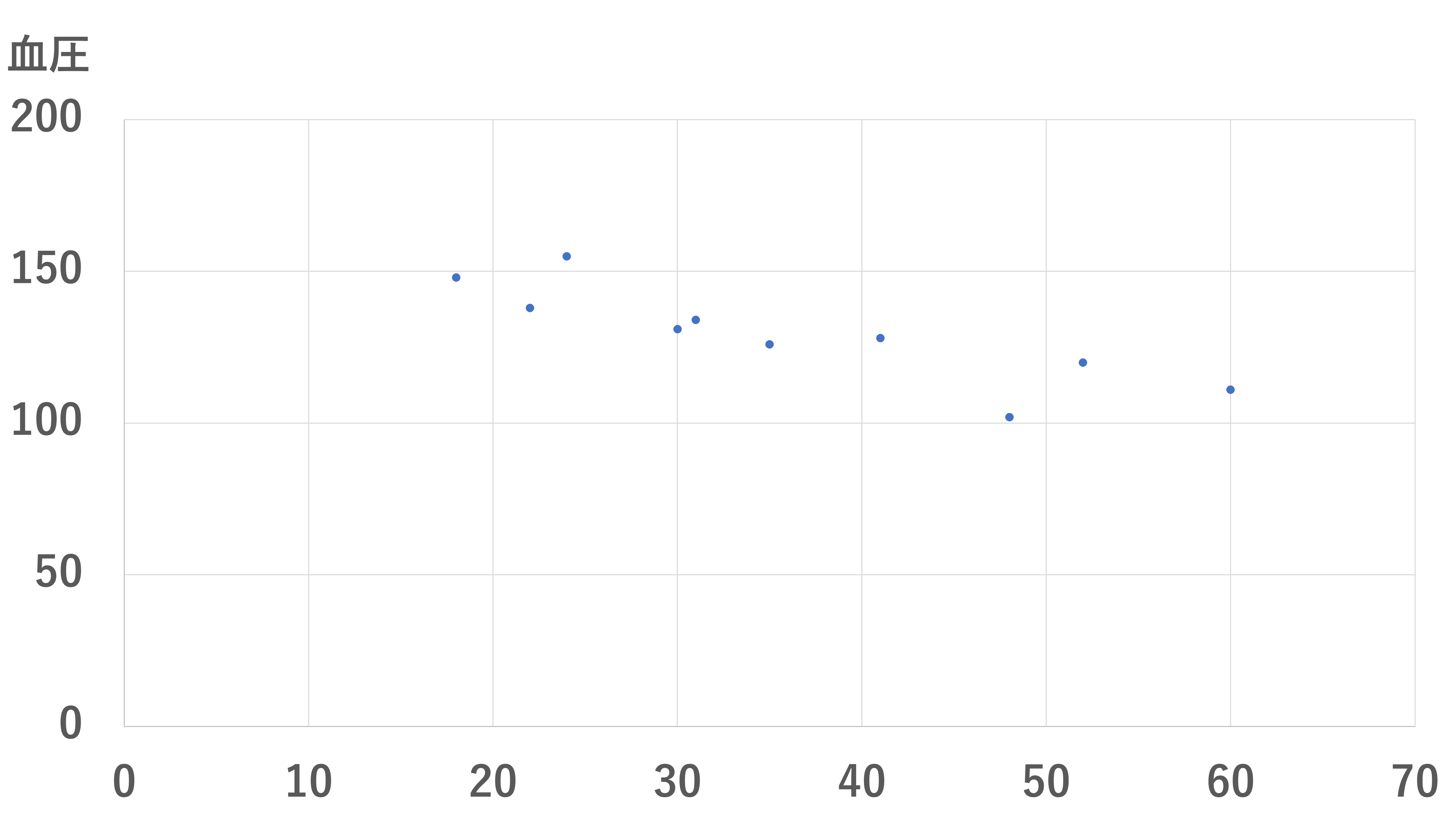
このように単相関係数がマイナスの場合は負の相関があると言います。一般的に負の相関と考えられている他の例としては、試験勉強時間と再試率などがあります。努力をしても報われないこともありますが、やらないよりかはやった方がマシでしょう。

 

最後に単相関係数が0に近い場合はどう考えればよいでしょうか？

 

 

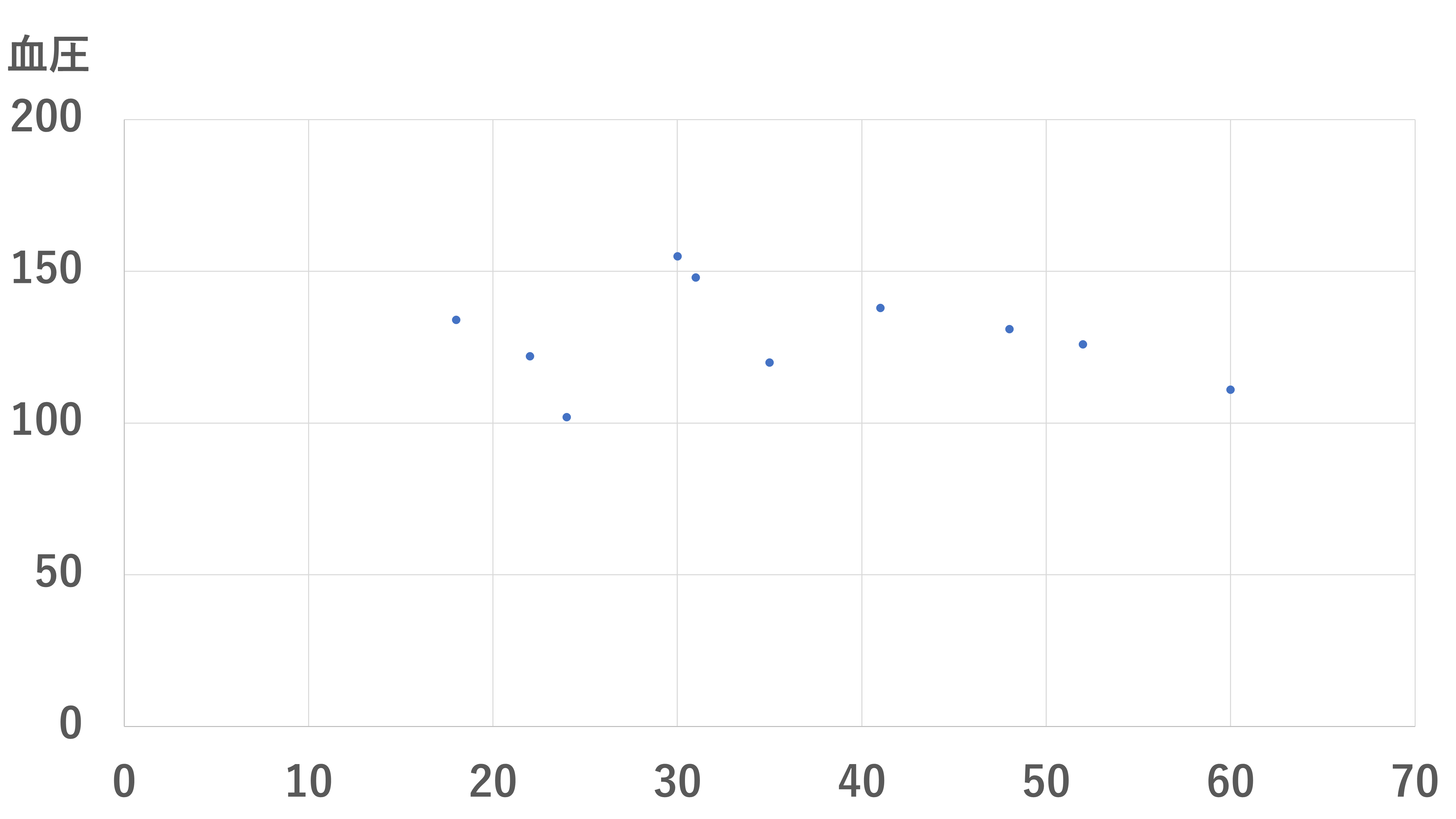
単相関係数が0に近い場合はグラフがいろいろなところに散らばっていて、2変数が関連していない、無関係であることを意味しています。今回の例でいえば、単相関係数が0に近ければ年齢と血圧は無関係と考えることができます。

 

 

単相関係数の基準

正の相関や負の相関を確認したところで、気になってくるのが単相関係数がどれくらいなら2変数が関連しているかということです。

 

実は単相関係数がいくらであれば関連していると言えるような基準はありません。参考程度ではありますが、単相関係数が以下のような場合関連性があるとされています。

 

• 0.9〜1；非常に強い関連
• 0.7〜0.9；やや強い関連
• 0.5〜0.7；やや弱い関連
• 0〜0.5；非常に弱い関連(無関係)

 

統計学をやっている時点で理系であり、理系あるあるとして白黒ハッキリさせたいところですが意外とあいまいになっています(笑)

 

まとめ

• 単相関係数の値がプラスの場合は正の相関がある、マイナスの場合は負の相関があると言う。
• 単相関係数が0に近い場合は、2変数が関連していないことを意味する。
• 単相関係数の具体的な基準はない。