Sponsored Link
標準偏差を用いて、データの特殊性を評価する
前回の基準値と偏差値では偏差値を見ました。今回は偏差値に関連して標準偏差をさらに深掘りしていきたいと思います。
偏差値62.7の意味
前回あなたの衛生の点数は63点で、偏差値が62.7ということが求まりました。平均点37.6点を上回っているので、明らかに喜んでいい点数なわけですが、どれくらい喜べばよいでしょうか？
そこで標準偏差を考えてみます。平均点37.6で標準偏差が20でしたので、37.6+20=57.6となります。つまりあなたがとった63点は標準偏差1個分くらい高い点数だったとわかります。標準偏差1個分では、月並みなデータなのでそこまで喜ぶことができないという結論になります。
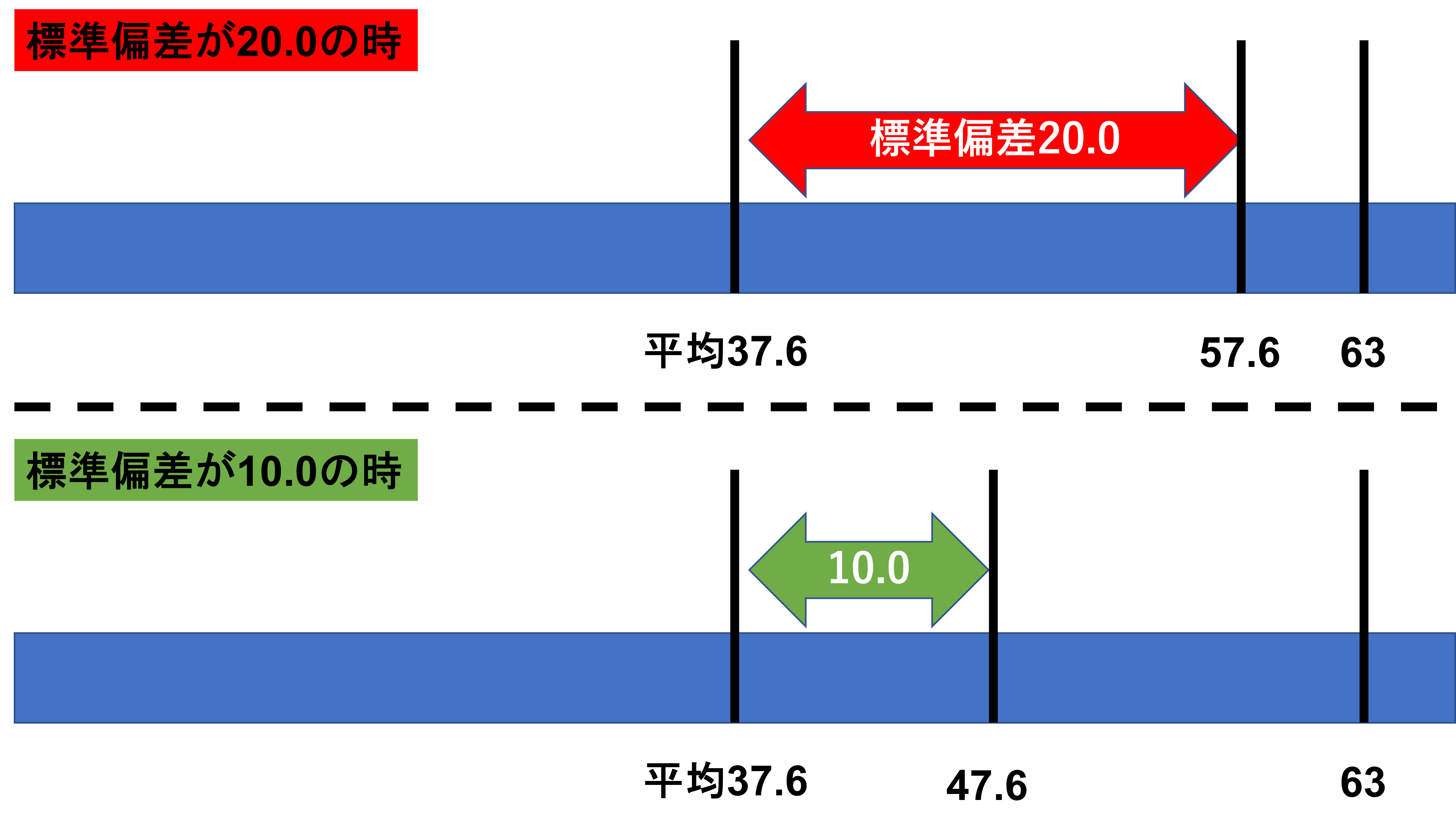
では、標準偏差が10だった場合はどうでしょうか？
同様に考えてみると、標準偏差一個分では37.6+10=47.6、標準偏差2個分では、37.6+10+10=57.6となります。あなたの63点は、標準偏差2倍以上離れていることになるので、これはかなり特別なデータであることがわかります。そのため、この場合は頑張ったご褒美などをもらえるくらい喜ぶべきデータになります。
Sponsored Link
Sponsored Link
データの特殊性
先ほどの例からもわかるように、標準偏差2個分以上離れているデータはかなり特殊であるということがわかりました。では具体的にどれくらい特殊なのでしょうか？
今後別ページでまとめようとは思っていますが、正規分布(今は左右対称の山のようなグラフと思っていてください)に近いものであれば、標準偏差1個分の範囲内に約70%のデータが入ります。そして、標準偏差2個分の範囲外に入るデータはわずか5%しかありません。
このことからも、標準偏差2個以上離れている場合はご褒美をしっかりもらわなくてはならないのです(笑)
では例題を見てみましょう。
例題
衛生と薬剤のテストの例では、友達の63点の方が価値が高いという結論だった。では、友達の63点は先ほどでいうところの特殊なデータなのか判断せよ。必要であれば、以下のデータを使え
薬剤
- あなた；49点
- 友達；63点
- 知人A；37点
- 知人B；28点
- 知人C；11点
- 薬剤の平均値37.6、標準偏差17.75
先ほどと同じようにやってみましょう。標準偏差1個分では37.6+17.75=55.35、標準偏差2個分では37.6+17.75×2=73.1
友達の63点は、標準偏差1個分と2個分の間にあるので、月並みなデータであるといえます。今、標準偏差1〜2個分ということでお茶を濁しましたが、モヤモヤする方のために、次の式でどれくらいのデータかわかります。
- (データ−平均値)÷標準偏差
例えば今回の友達の例でいくと、
(63−37.6)÷17.75=1.43
つまり友達は平均値から標準偏差1.43個分だけ離れていたということになります。
まとめ
- 標準偏差2個以上離れているデータは正規分布する場合前回の5%しか存在せず、かなり特殊なデータと言える。
就職や転職でお悩みの方はコチラ！私はここで年収120万円上がりました
Sponsored Link
標準偏差を用いて、データの特殊性を評価する 関連ページ
- 母集団と標本
- 統計学とは、簡単に言うと標本の情報から母集団の状況を推測する学問です。母集団とは本来調査するべき全員を指し、その一部を標本ということができます。
- 数量データとカテゴリーデータ
- 統計学では、目盛が等間隔で測れるデータを数量データと言います。目盛が等間隔ではなく測れないものをカテゴリーデータと言います。
- カテゴリーデータと単純集計表
- カテゴリーデータをまとめたものは単純集計表と呼ばれることがあります。単純集計表の作り方は、カテゴリーデータの各項目を数えて、割合を出すことで作られます。
- 度数分布表の作り方、基礎編
- データから度数分布表の作り方は、最大値と最小値を把握する、階級を決める、階級値を決める、度数を数える、相対度数を出すというように行います。
- ヒストグラムの作り方、基礎編
- ヒストグラムとはいわゆる棒グラフのことで、横軸は階級値、縦軸は度数(相対度数)などにより描かれます。度数分布表やヒストグラムを作ることで、より直感的にデータの特徴を感じることができます
- 度数分布表とヒストグラム、例題編
- 今まで見てきた度数分布表とヒストグラムの作り方をもとに、例題を交えてさらに理解できるようにします。度数分布表とヒストグラムを慣れるまで繰り返しましょう。
- 平均値と中央値の違い
- 平均値とはデータの合計値を全データで割ったもので、中央値はデータを小さい順から並べたときに真ん中にくるものです。そのため平均値と中央値は違います。
- 分散とは？
- 平均値のみではデータの散らばりの判断がつかないので、分散を知る必要があります。分散は偏差の二乗の合計値を全データで割って求めることができます。
- 標準偏差、基礎編
- 分散の欠点を解消するために√をとったものが標準偏差であり統計学ではかなり重要です。標準偏差は0であればデータが全く散らばっていなく、大きくなるほど散らばっていることを示しています。
- 標準偏差、例題編
- 標準偏差の求め方は、平均値を出す、偏差を出す、分散を出す、標準偏差を出すという手順で出すことができます。薬学部において標準偏差を出すことができればかなりの進歩です。
- 統計学で偏差値を考える
- CBTや国家試験の模試を行うと、偏差値が出てきます。統計学の平均値や標準偏差の知識を用いることで、テストの偏差値や1点の重みがわかります。
- 基準値と偏差値
- 偏差値は基準値×10+50で出すことができます。偏差値は基準値をもとにして出されるので、満点の点数が違うものや、単位が違うものも比較できます。
- データに一定数を加えた時の平均値や標準偏差への影響
- データに一定数を加えて加工すると平均値のみ変化して標準偏差には影響を与えません。これはヒストグラムがただ横にスライドするだけと考えるとわかりやすいでしょう。
- データに一定数をかけた時の平均値や標準偏差への影響
- データに一定数をかけた場合、平均値も標準偏差もかけた数だけ増えます。つまり没問が出た場合、標準偏差にも影響が出てしまうため得点を二倍にしてはいけません。
- 正規分布の式とグラフ
- ヒストグラムの階級を限りなく狭めていくと曲線になっていき、その曲線の式を確率密度関数といいます。正規分布は確率密度関数の1つで左右対称の山のようなグラフとなります。
- 標準正規分布と性質
- 平均が0で標準偏差が1の時は、xは標準正規分布に従います。正規分布の特性としてμ±σの範囲のデータの相対度数は約70%がこの中に入り、μ±2σの範囲のデータの相対度数は約95%がこの中に入ります。
- 標準正規分布の95%予言的中区間
- 標準正規分布は無限の数字をとる可能性がありますが、その性質を利用することで次に出てくるデータを推測することができます。標準正規分布の95%予言的中区間は−1.96〜＋1.96です。
- 正規分布の95%予言的中区間と例題
- 標準正規分布のデータに一定数σをかけて、さらに一定数μを足して加工するため、正規分布の95%予言的中区間は、μ−1.96σ〜μ+1.96σです。
- 標準正規分布表、面積と確率
- 標準正規分布表は、横軸の値と確率密度関数のグラフで囲まれる面積がどれくらい占めているのかを表しています。またこの面積は確率と等しくなります。
- データから母集団を推定する方法
- 正規分布の95%予言的中区間を使うことで、データから母集団を推定することができます。この時に、仮説が妥当ではない場合は仮説を棄却すると統計学では言います。
- 95%信頼区間とは
- 95%信頼区間とは様々な観測値から同じ方法で区間推定をして、そのうち95%は正しい母数を含んでいるものを言います。−1.96≦(N−μ)/σ≦+1.96で95%信頼区間は求めます
- 無作為抽出の仮定と母平均
- 無作為抽出の仮定を用いると、階級値×相対度数の合計=平均値をあてはめることができ、ここから出した平均値を母平均といいます。
- 母標準偏差の出し方
- 度数分布表から母分散を出す場合、(偏差の二乗×相対度数)の合計で出す必要があります。また母分散に√(ルート)をとったものが母標準偏差です。
- 標本平均とは
- 1つの母集団からn個のデータを観測して標本平均を作ると、nが大きいほど標本平均は母平均に近い数値をとる可能性が高くなります。
- 正規分布している母集団からの標本平均における95%予言的中区間
- 母集団が正規分布している場合は、そこから標本平均を作った場合も正規分布します。正規分布している母集団からの標本平均における95%予言的中区間はμ−1.96σ/√n〜μ+1.96σ/√nです。
- 標本平均から母集団の母平均を推定する
- 観測データから母集団の母平均μを推測する場合は、95$信頼区間を利用して、標本平均が予言の範囲に入るような母平均を持つ母集団のみ妥当なものとして残す
- 標本分散の性質
- 標本分散=｛(偏差1)^2+(偏差2)^2+・・・・+(偏差n)^2｝/nで表されます。分子も分母も必ずプラスになるため、標本分散は必ずプラスとなり正規分布しなくなります。
- カイ二乗分布とは？自由度とヒストグラム
- 標本分散はカイ二乗分布となり自由度は、標本数を表します。カイ二乗分布のヒストグラムは自由度によって形が変化していきます。
- カイ二乗分布表の読み方と例題
- カイ二乗分布表は標準正規分布表とは異なり、横軸以上の面積が占める割合を表しています。カイ二乗分布表の読み方と例題をまとめてみました。