無作為抽出と乱数表

前回の母集団と標本では、母集団の状況を標本から推測するのが統計学という話をしました。今回は標本についてもう少し細かく見ていきます。

 

 

標本のデータの記録

観測した標本データは、わかりやすく分析しやすいように記録する必要があります。例を見てみましょう。

 

例えば、ある薬学部の学生の身長のデータを集めたとします。統計学では一般的には以下のような形で記録します。

 

 

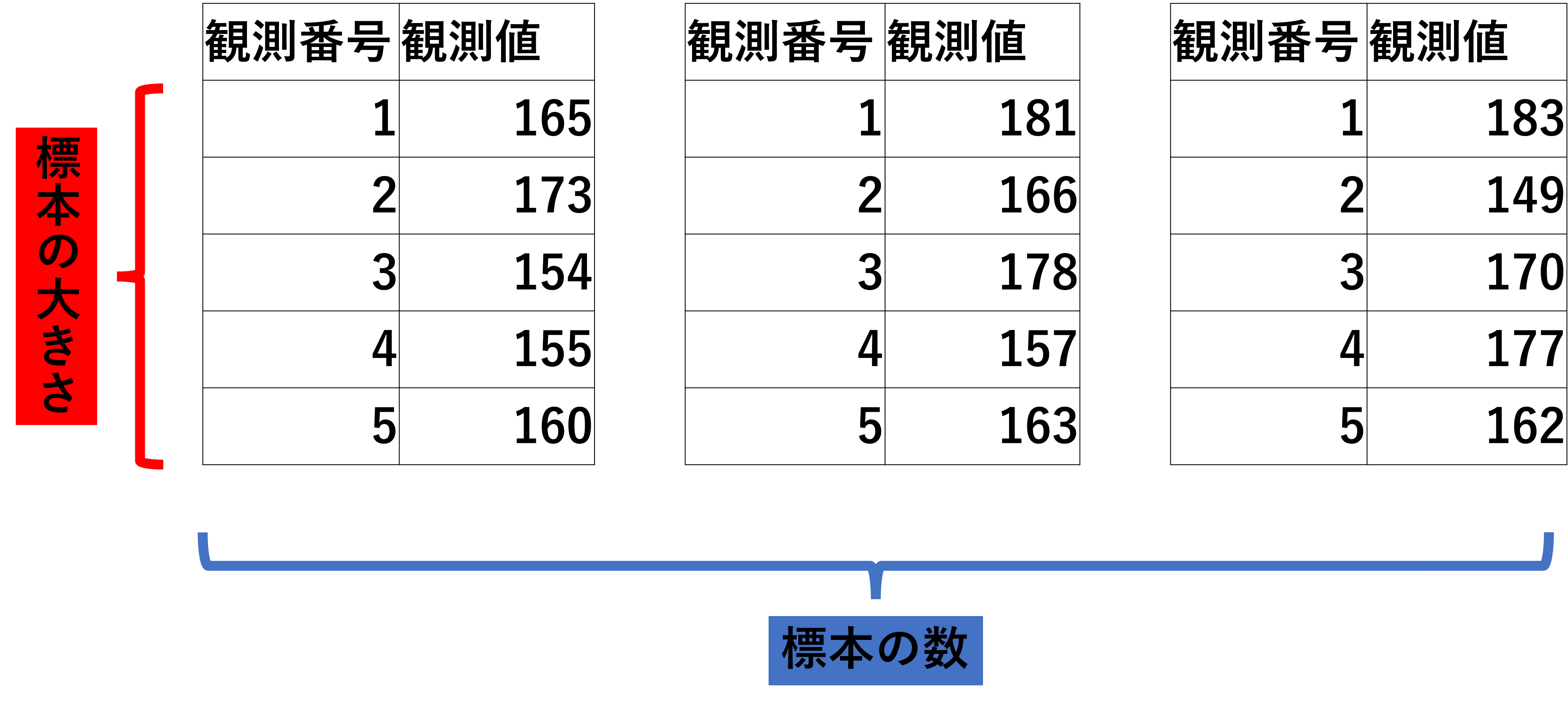
左側には観測番号、右側には観測値を書いていきます。1つの標本に含まれる観測データの数のことを標本の大きさ(標本サイズ)と言います。今回の例で言うなら、標本の大きさは5といえます。

 

ではこの標本の大きさ5を3セット集めたとしましょう。このセット数のことを標本の数と言います。

 

 

無作為標本

一般的には女性より男性の方が身長が高いため、先ほどの身長の例において男性ばかりを選んでしまうと、身長が高いデータができあがる可能性が高くなってしまいます。そのため母集団から標本を選ぶには、偏りがないようにする必要があります。

 

どのような基準から見ても、偏りのない標本を選ぶ方法を無作為抽出と言います。そして、無作為抽出で選ばれた標本を無作為標本と言います。

 

無作為抽出をするためには、乱数表と呼ばれる特別な表を使います。乱数表は名前の通りランダムに数字が並んでいる表で、これを読み取ることで無作為標本を抽出します。

 

 

今回は数の少ない簡単なもので読み取り方を見ていきます。

 

横方向を「行」、縦方向を「列」と呼びます。なんでもいいのですが、例えば自分の誕生日が25日だとしたら、行は2、列は5のところをみます。そうすると、12であるので12の人を抽出するといった具合に使います。先ほどの12を起点に左に5人分抽出すると、12、2、9、17、10となります。

 

今回は簡単な表なので左に5人分しかできませんでしたが、もっと大きい乱数表では、上下左右色々な数字があるので自分で起点の数字から上に5人、下に5人、右に5人などあらかじめルールを決めて選び続けることで無作為抽出が可能となります。

 

今回はわかりやすいように、乱数表も1〜25の数字を1つずつ選んだので重複することはありませんでしたが、もっと大きい乱数表では抽出を続けていくと同じ数が複数回出てくることがあります。この時に、同じ数を何度でも選ぶ方法を復元抽出法、同じ数は使わずに捨てる方法を非復元抽出法と呼びます。

 

まとめ

• 母集団から標本を選ぶときには、偏りがないようにする必要がある。
• 無作為抽出するために乱数表を用いる