カテゴリーデータと単純集計表

前回の数量データとカテゴリーデータでは、統計学に使われるデータの種類について見ました。今回は統計学の手始めとして、カテゴリーデータについて深掘りしたいと思います。

 

 

単純集計表

まずカテゴリーデータの復習です。カテゴリーデータは、測ることのできないデータを言うのでした。前回の例でいうなら、当サイトのわかりやすさのアンケートがカテゴリーデータです。では架空のデータですが、その当サイトのわかりやすさのアンケート結果が以下のようになったとします。

 

 

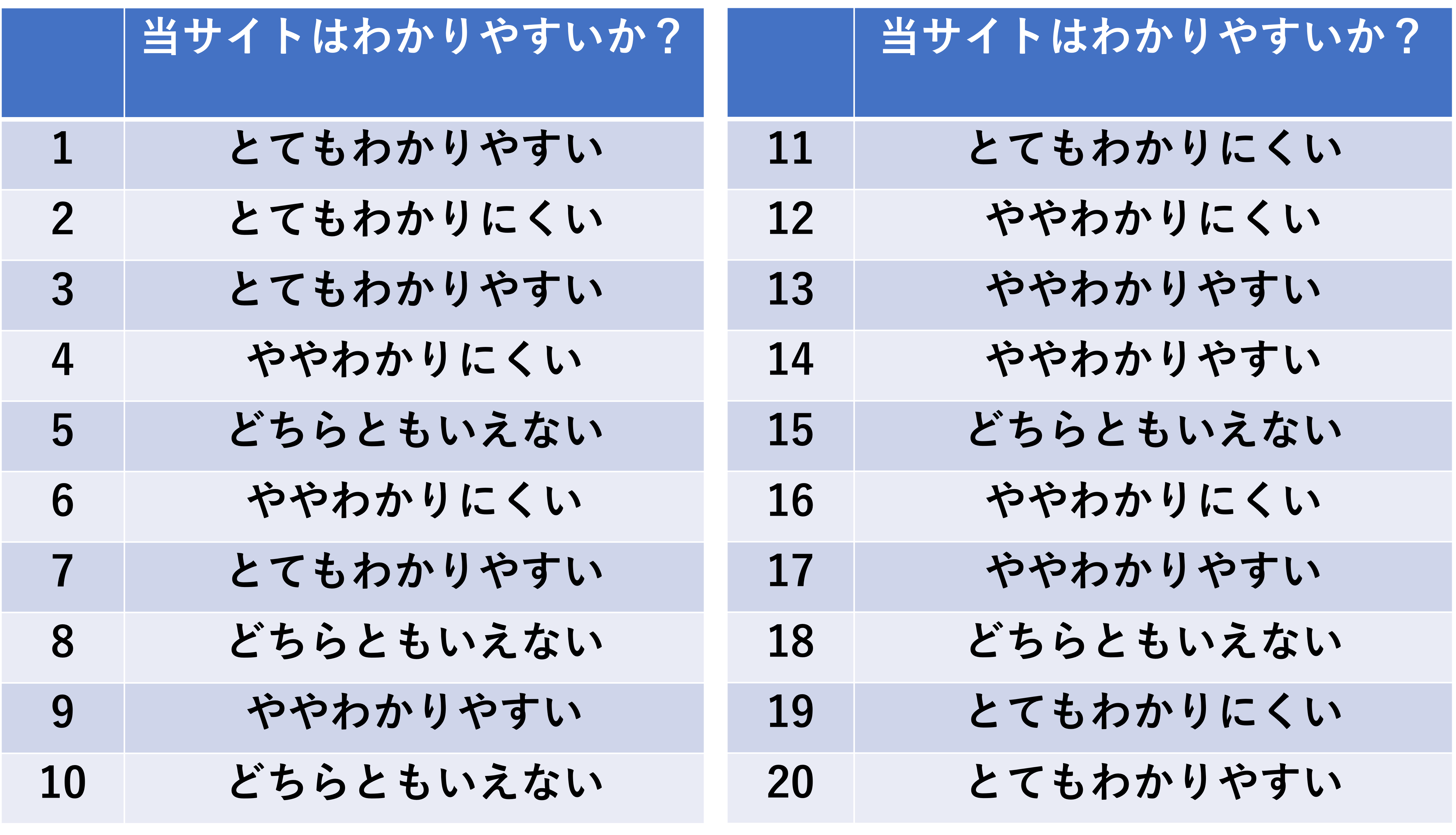
このままでは、各項目どれくらいの人数いるのかわかりにくいので数えます。数え方は間違えなければなんでもいいですが、シンプルに最初の1番の人から、集中して正の字で数えていくのが良いと思います。

 

 

順調に数えられたら以下のようになっていると思います

 

 

• とてもわかりやすい；5人
• ややわかりやすい；3人
• どちらともいえない；5人
• ややわかりにくい；4人
• とてもわかりにくい；3人

 

一応間違え確認のために、集計が終わった後に各項目を足して全データ数になっているか確認した方がテストなどでは安心です。今回の場合すべて合わせて20人なので、各データの合計が20人で一致しているのであっていますね。

 

さらに各項目の人数を全データ数で割ると、その項目が何%占めているかがわかります。例えば、とてもわかりやすいの場合は5人なので、5÷20=0.25。つまり25%占めていることがわかります。これを各項目やっていくと、以下のようになるかと思います。

 

とてもわかりやすい；5人。割合25%
ややわかりやすい；3人。割合15%
どちらともいえない；5人。割合25%
ややわかりにくい；4人。割合20%
とてもわかりにくい；3人。割合15%

 

これを少しわかりやすく表にまとめると、次のようになります。

 

 

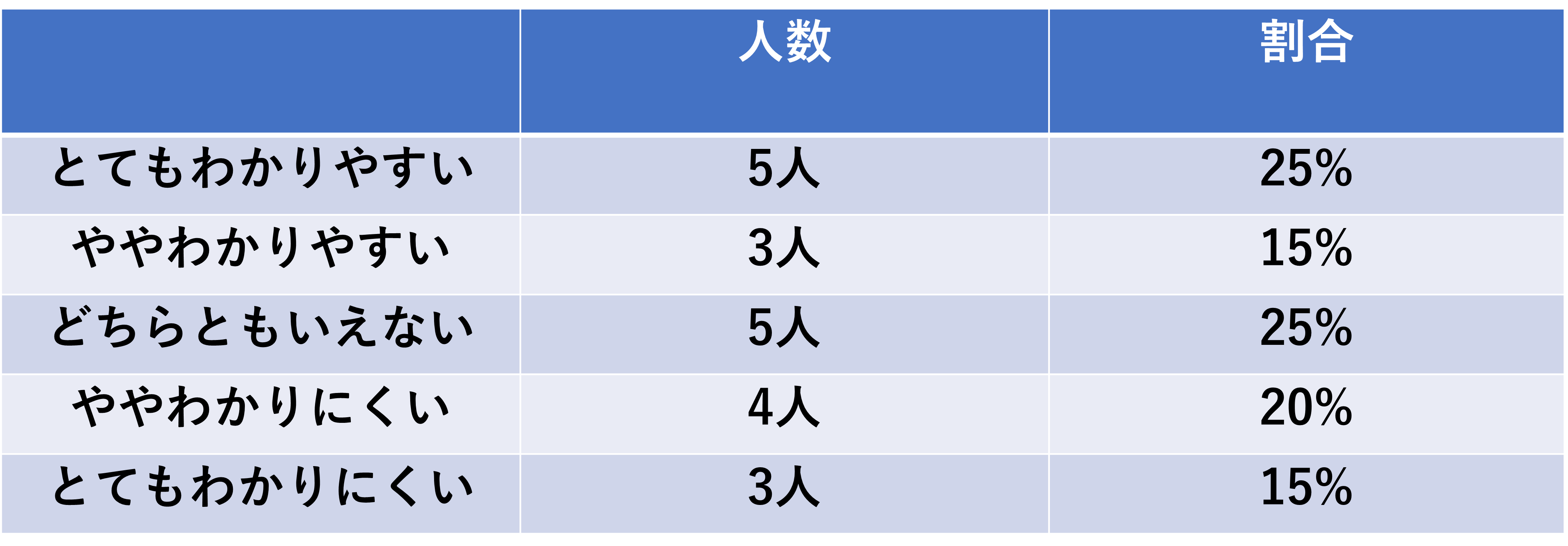
この表を単純集計表と呼ぶこともあります。ではこの単純集計表をもとにわかりやすくするためにグラフにしてみます。

 

 

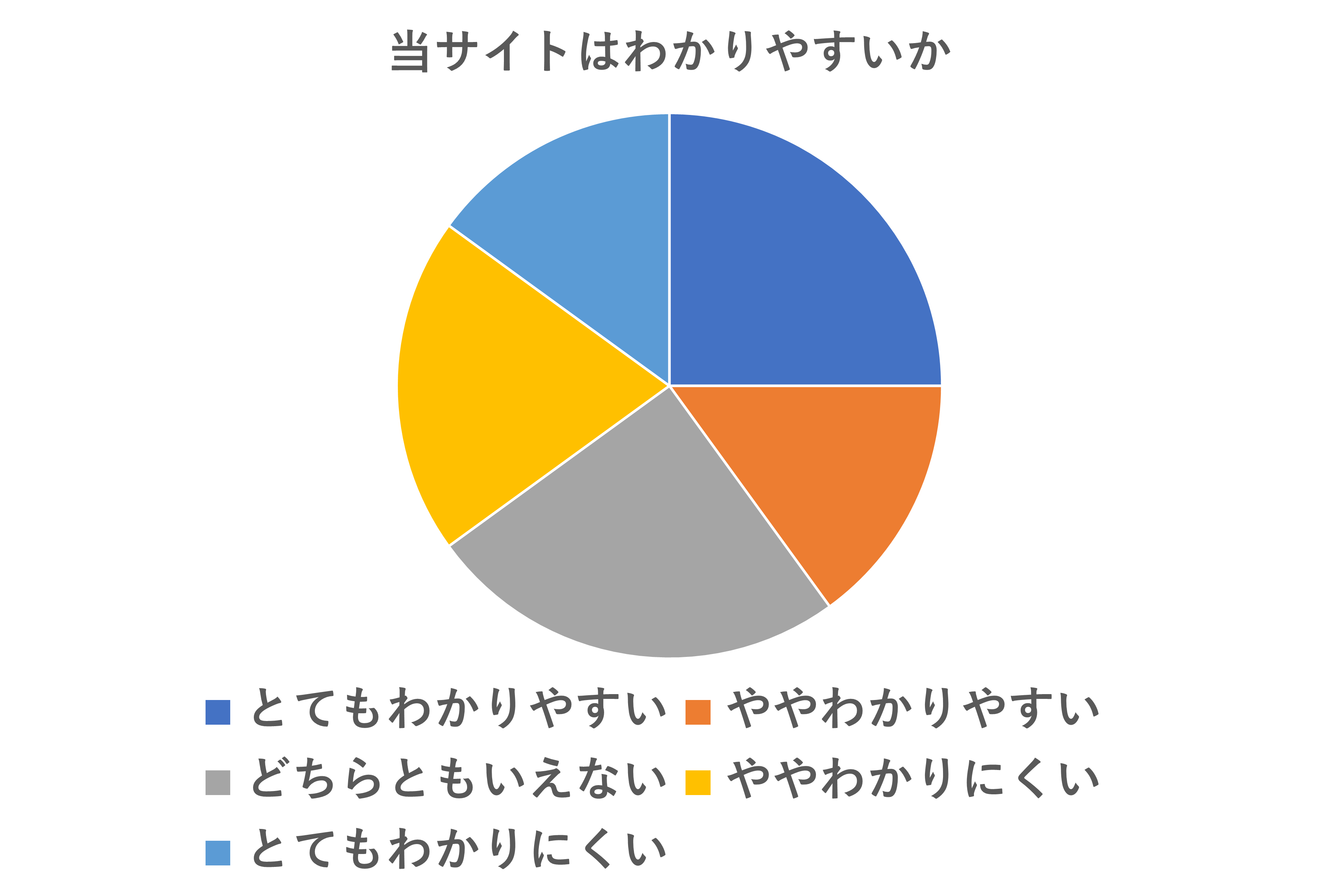
グラフ化することで、アンケート結果が一目瞭然ですね。

 

では例題で練習してみましょう

 

例題

当サイトのアンケートを行った人の血液型のデータは以下のようになった。このデータにおける単純集計表を作れ

 

 

先ほどと同様に各血液型の人数を数えましょう

 

A；7
B；5
O；5
AB；3

 

そして、次に割合を求めます。

 

A；7。割合35%
B；5。割合25%
O；5。割合25%
AB；3。割合15%

 

よって単純集計表は以下のようになります。

 

 

まとめ

• カテゴリーデータをまとめたものは単純集計表と呼ばれることがある。