Sponsored Link
度数分布表とヒストグラム、例題編
前回のヒストグラムの作り方、基礎編では、度数分布表からヒストグラムの作り方についてみました。今回は度数分布表とヒストグラムの例題編となります。もし前回までで十分理解できてるよという方でしたら、今回のページもほぼ同じなので読み飛ばしていただいて構わないです。
では早速例題です。
例題
当サイトにおけるアンケート内容で年齢を集めたところ以下のようなものが集まった。
以下の問いに答えよ
- 階級、階級値、度数、相対度数、累積度数を含めた度数分布表を作成しなさい
- 度数分布表をもとに縦軸が相対度数のヒストグラムを作成しなさい
Sponsored Link
Sponsored Link
階級、階級値、度数、相対度数、累積度数を含めた度数分布表を作成しなさい
度数分布表を作る手順は以下の通りでした。
- 最大値と最小値を把握する
- 階級を決める
- 階級値を決める
- 度数を数える
- 相対度数を出す
最大値と最小値を把握する
最大値は39、最小値は18です。
階級を決める
18〜39なので、今回も区切りがよいように5きざみでよいかと思います。
- 16〜20
- 21〜25
- 26〜30
- 31〜35
- 36〜40
階級値を決める
階級値は階級の真ん中の値でした。なので
- 16〜20；階級値18
- 21〜25；階級値23
- 26〜30；階級値28
- 31〜35；階級値33
- 36〜40；階級値38
となります。
度数を数える
度数は各階級にあるデータの数でした。なので
- 16〜20；階級値18；度数4；累積度数4
- 21〜25；階級値23；度数8；累積度数12
- 26〜30；階級値28；度数15；累積度数27
- 31〜35；階級値33；度数8；累積度数35
- 36〜40；階級値38；度数5；累積度数40
となります。
相対度数を出す
相対度数は、度数を全データで割ったものでした。なので
- 16〜20；階級値18；度数4；累積度数4；相対度数0.1
- 21〜25；階級値23；度数8；累積度数12；相対度数0.2
- 26〜30；階級値28；度数15；累積度数27；相対度数0.375
- 31〜35；階級値33；度数8；累積度数35；相対度数0.2
- 36〜40；階級値38；度数5；累積度数40；相対度数0.125
となります。
度数分布表をもとに縦軸が相対度数のヒストグラムを作成しなさい
ヒストグラムは横軸が階級で、縦軸は度数か相対度数の棒グラフでした。今回は相対度数で作るので、以下のようなヒストグラムとなります。
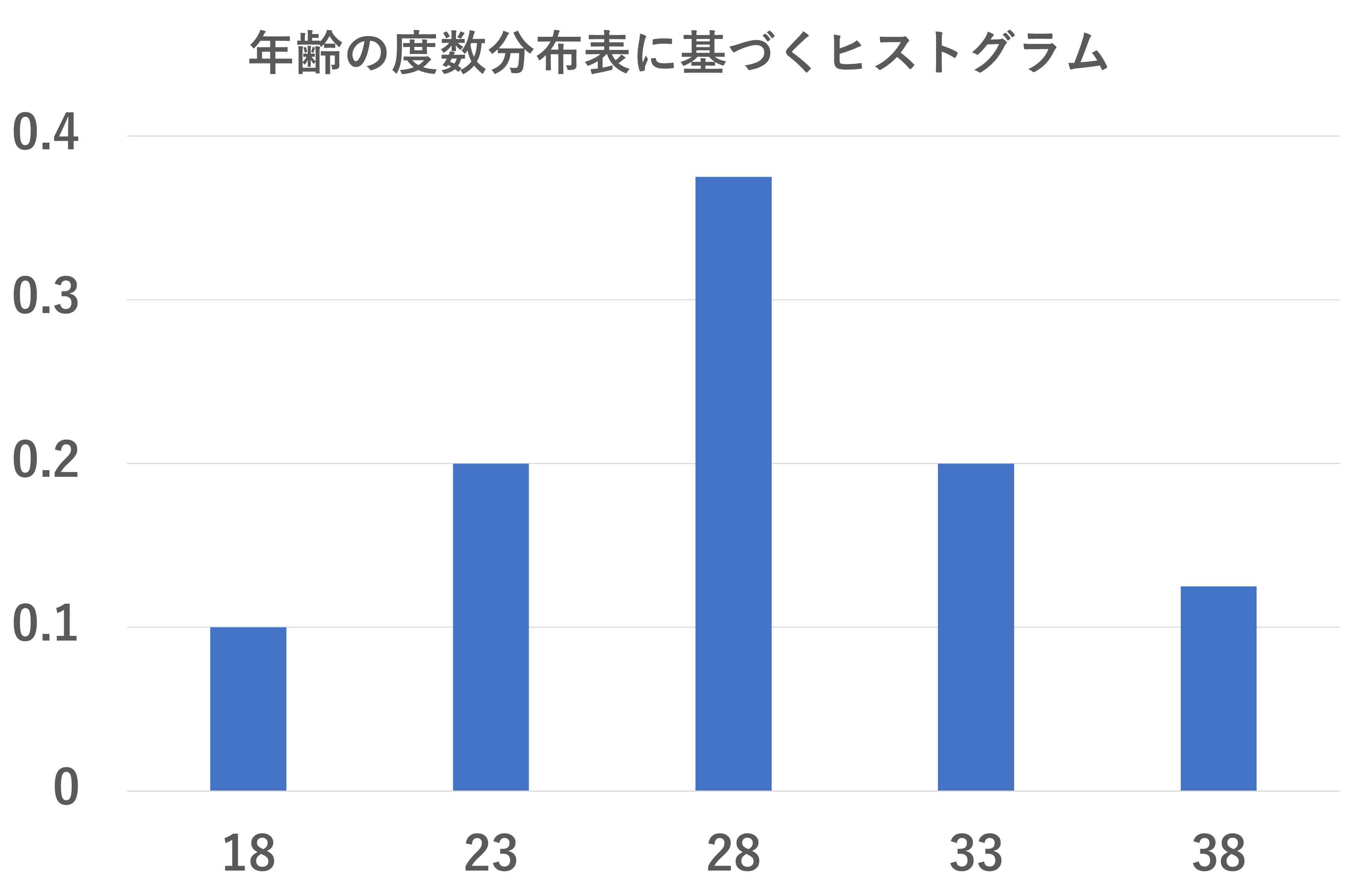
ヒストグラムを作ることで、以下のような特徴が見えてくると思います。
- 26〜30にデータが集まっている。
- 26〜30を起点にして年齢が低い方にも高い方にも左右対称にデータが分布している。
どうでしょうか？より度数分布表とヒストグラムの理解が深まりましたでしょうか？慣れてくると単純作業かと思うので、何回も繰り返し練習しましょう。
まとめ
- 度数分布表とヒストグラムの作成を何度も行い慣れましょう
就職や転職でお悩みの方はコチラ！私はここで年収120万円上がりました
Sponsored Link
度数分布表とヒストグラム、例題編 関連ページ
- 母集団と標本
- 統計学とは、簡単に言うと標本の情報から母集団の状況を推測する学問です。母集団とは本来調査するべき全員を指し、その一部を標本ということができます。
- 数量データとカテゴリーデータ
- 統計学では、目盛が等間隔で測れるデータを数量データと言います。目盛が等間隔ではなく測れないものをカテゴリーデータと言います。
- 度数分布表の作り方、基礎編
- データから度数分布表の作り方は、最大値と最小値を把握する、階級を決める、階級値を決める、度数を数える、相対度数を出すというように行います。
- ヒストグラムの作り方、基礎編
- ヒストグラムとはいわゆる棒グラフのことで、横軸は階級値、縦軸は度数(相対度数)などにより描かれます。度数分布表やヒストグラムを作ることで、より直感的にデータの特徴を感じることができます