熱力学4、エントロピーとは？熱力学第二法則との関係

前回の熱力学3、エンタルピーとは？ヘスの法則の計算ではエンタルピーについてまとめました。その時にややこしい言葉として「エントロピー」があるという話をしました。今回はエントロピーについて見ていきたいと思います。

 

 

エントロピーとは

エントロピーとは乱雑さの指標となるもので、示量性状態関数の1つです・・・と言っても乱雑さがよくわからないと思うので例を見ていきます。

 

例えば、コーヒーにミルクを入れるとはじめは固まっていますが、そのうち混ざりあってきます。実際には、スプーンでかき混ぜてあっという間に混ざってしまいますが、はじめは一か所にまとまっています。時間が経つにつれてミルクが、コーヒーの中へと均一に散らばっていきます。これを乱雑な状態と言います。

 

ここで、コーヒーの中に混ざってしまったミルクは時間が経つと、また元に戻るでしょうか？もとに戻らず混ざったままですよね。このように自然におこる変化はもとに戻らず不可逆的です。エントロピーは与えられた条件で、どれだけもとに戻りにくいかということを表しているのです。

 

 

熱力学第二法則

エントロピーに関連した法則として熱力学第二法則があります。熱力学第二法則は系の自発性と平衡に関する法則であり、以下のような表現がされます。

 

• 少しも変化を残さないで、熱をそれと等量の仕事に変換することはできない。
• 孤立系において自発的に起こる変化は不可逆でエントロピーが増大する。
• 外界に何の変化も残さずに、低温物質から高温物質に熱が流れることはない。

 

要するに熱力学第二法則は、「仕事をするにあたって、必ず無駄が出てくるよ」「物事は必ず散らかる方向に進むよ」ということを言っています。

 

熱力学第三法則

熱力学第二法則の他にも、エントロピーに関わるものに熱力学第三法則があります。熱力学第三法則は完全結晶性物質のエントロピーは0Kで0であるというものです。つまり、−273℃ではエントロピーは0と言い換えることもできます。

 

水の相変化に対するエンタルピーとエントロピーの変化

ここまでやったら、エンタルピーとエントロピーは全然違うものというのがわかったと思います。そのまとめとして、水の相の変化とエンタルピーとエントロピーの変化について見てみましょう。

 

 

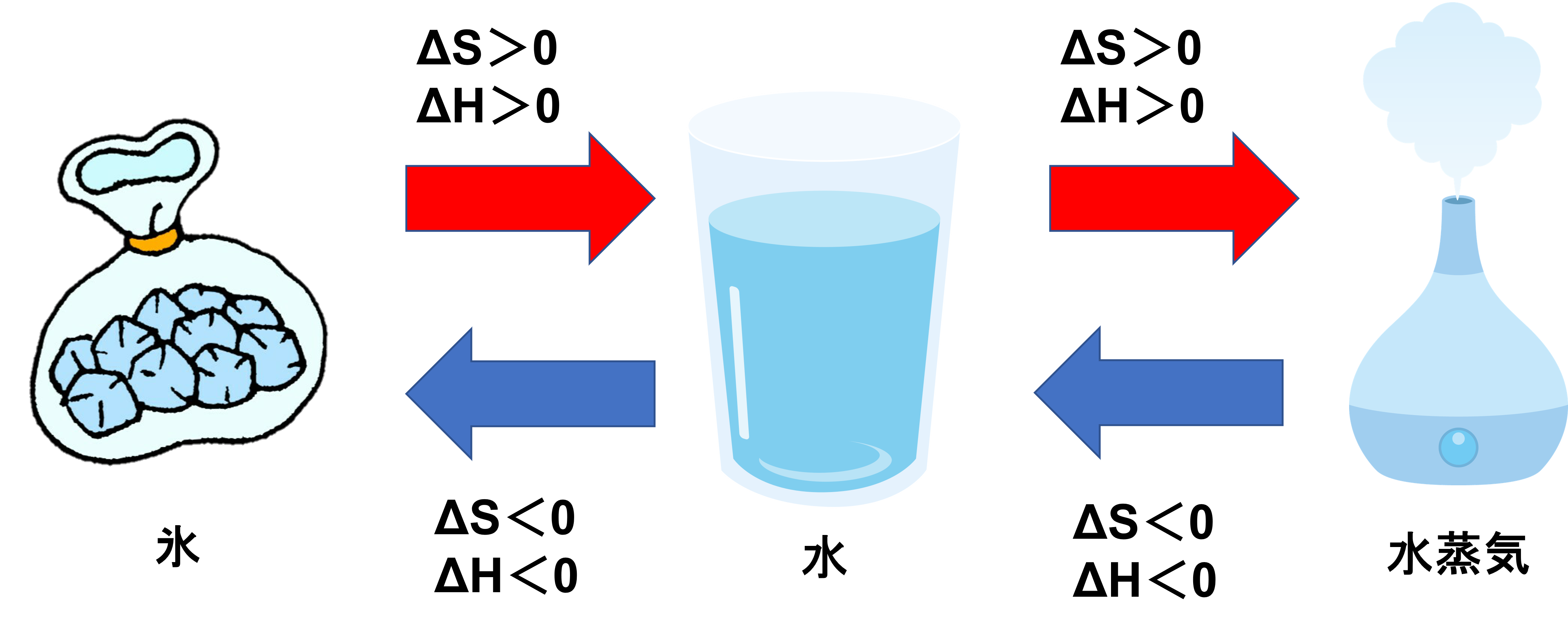
• 固体(氷)から液体(水)への変化；ΔH＞0、ΔS＞0
• 液体(水)から気体(水蒸気)への変化；ΔH＞0、ΔS＞0
• 気体(水蒸気)から液体(水)への変化；ΔH＜0、ΔS＜0
• 液体(水)から固体(氷)への変化；ΔH＜0、ΔS＜0

 

エンタルピーについてはΔH＞0は吸熱反応で、ΔH＜0は発熱反応でしたね。それがわかっていれば、吸熱することで固体から液体、さらには気体になっていくのがわかると思います。逆に発熱することで、気体から液体、固体へと変わっていきます。

 

エントロピーについては、ギューッとしている固体から、バラバラとしている気体になるため、ΔS＞0となります。また逆にバラバラしている気体から、ギューッとしている固体になるのはΔS＜0であることがわかります。

 

まとめ

• エントロピーは乱雑さの指標
• 熱力学第二法則では、仕事をするにあたって必ず無駄が出てくる、物事は必ず散らかる方向に進むということを示している。
• エンタルピーとエントロピーの違いを正しく理解しよう。