共沸点を持つ場合の状態図

前回の2成分の気液平衡の状態図では、2成分の気液平衡について見ました。今回は応用編の共沸点を持つ状態図について見ていきます。

 

 

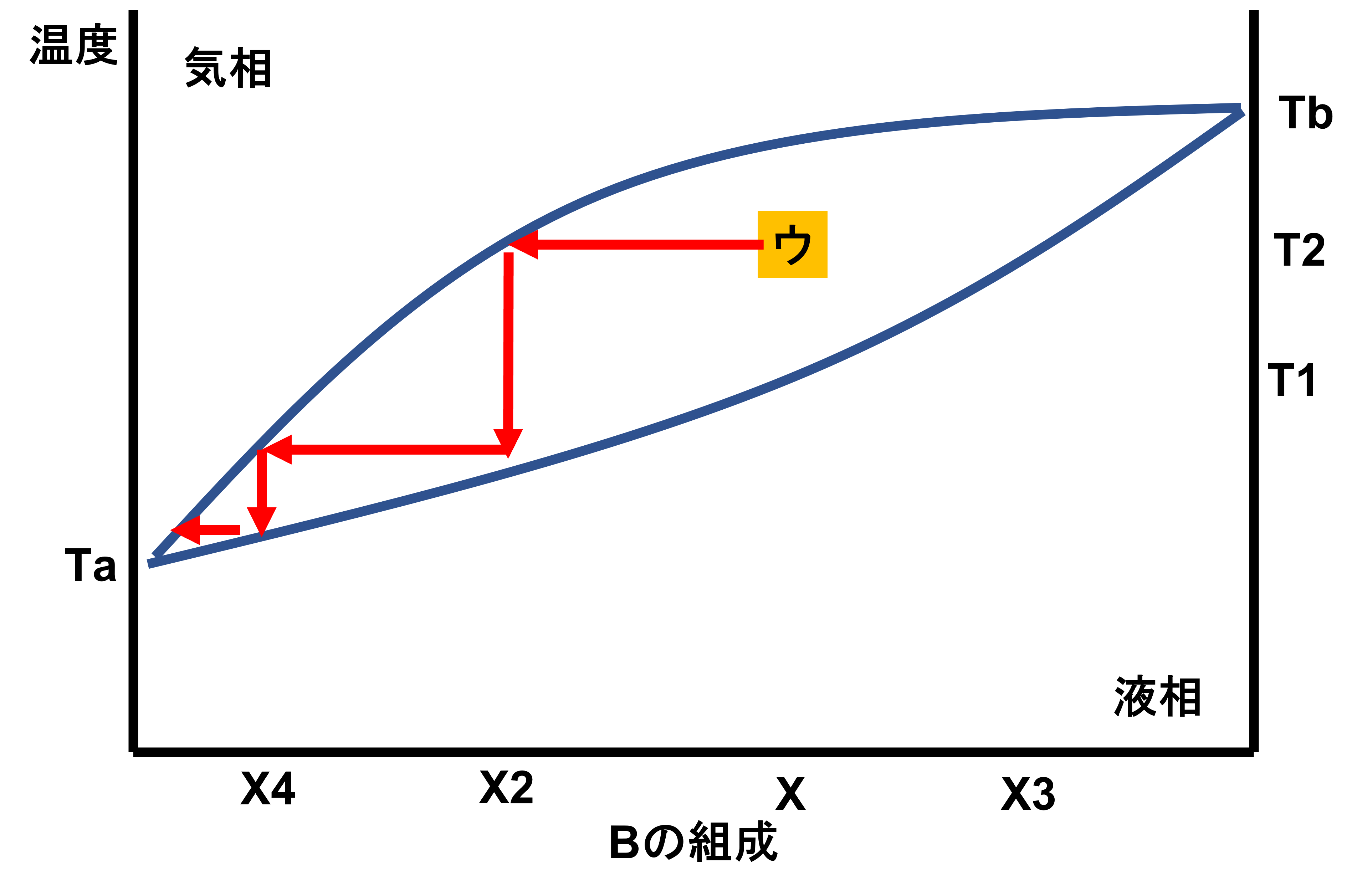
共沸点を持つ場合の状態図

一部の物質では混合物であるにも関わらず沸点を持つものがあり、以下のような状態図をとります。

 

 

• 上の曲線；気相線
• 下の曲線；液相線
• Ta；Aの沸点
• Tb；Bの沸点
• T0；共沸点
• X0；共沸混合物中のBの組成

 

共沸点を持つ場合での状態図では、X0を境に左にあるのか、右にあるのかでわけて考えることが重要です。そうしたら、後は前回と同じ考え方で対応できます。割愛するので蒸留を繰り返した場合の結論です。

 

 

• X0より左側にある場合；蒸気からは純物質Aが回収できる。残留した液体からは共沸混合物が回収できる。
• X0より右側にある場合；蒸気からは純物質Bが回収できる。残留した液体からは共沸混合物が回収できる。

 

ここまでは前回をしっかりやっていれば問題ないかと思います。では、次にこの状態図ではAとBを混ぜた場合、発熱反応でしょうか？吸熱反応でしょうか？

 

混合することによって液相の安定化が起こり発熱が見られます。そのため、共沸点は各成分の沸点より高くなります。つまり発熱反応では上にとんがったグラフとなります。逆に下にとんがったグラフでは反対のことが起こるので吸熱反応となります。

 

 

では今回も国試風の例題を見てみましょう。

 

 

例題

図は成分Aと成分Bの混合系の気液平衡の状態図である。圧力一定の時、横軸は成分Aのモル分率、縦軸は温度である。この混合系に関する記述の正誤について答えよ。

 

 

1. 成分Aのモル分率が0.3の混合物は、分留によって共沸混合物と成分Aにわけられる
2. 成分Aと成分Bを混合すると、発熱する。
3. 相の数をP、自由度をFとすると、F=3−Pである。

 

成分Aのモル分率が0.3の混合物は、分留によって共沸混合物と成分Aにわけられる

×。成分Aのモル分率が0.3の混合物の分留は、左側のみで考えればよかったですね。蒸留を繰り返していくことによって、成分Aの組成が0に近づいていくため、蒸気からは純物質Bと、残留した液体からは共沸混合物が回収できます。

 

成分Aと成分Bを混合すると、発熱する。

〇。発熱の時は上にとんがったグラフ、吸熱の時は下にとんがったグラフでしたね。そのためこのグラフでは発熱します。

 

相の数をP、自由度をFとすると、F=3−Pである。

×。自由度(F)=成分の数(C)−相の数(P)＋2でした。今回は成分Aと成分Bと2成分であるため、C=2となります。これを代入すると、F=2−P+2となり、F=4−Pとなります。

 

まとめ

• 共沸点をもつ状態図の場合では、左と右にわけて考えれば前回と同じ考え方で対応できる。