熱力学5、ギブズ(Gibbs)エネルギーとは？

前回の熱力学4、エントロピーと熱力学第二法則ではエントロピーについて見ました。今回はギブズ(Gibbs)エネルギーについて見ていきたいと思います。

 

 

ギブズ(Gibbs)エネルギー

ある温度で自発変化の方向は系のエンタルピーとエントロピーの変化で決まります。それぞれの関数で表されたものがギブズ(Gibbs)エネルギーであり、以下の式で表されます。

 

• G=H−TS

 

 

エンタルピー(H)の単位はJ、温度(T)の単位はK、エントロピー(S)の単位はJ/Kであるため、ギブズ(Gibbs)エネルギーの単位はJとなります。

 

さてギブズ(Gibbs)エネルギーの式のTSですが、これは束縛エネルギーと呼ばれて仕事につかえないエネルギーを表しています。つまり、ギブズ(Gibbs)エネルギーは全エネルギーであるエンタルピーから仕事に使えないエネルギーを引いているので仕事に使うことのできるエネルギーを表しているとも言えます。

 

 

ギブズ(Gibbs)エネルギーの変化量が意味すること

ギブズ(Gibbs)エネルギーの変化量のΔGは以下の式で表されます。

 

• ΔG=ΔH−TΔS

 

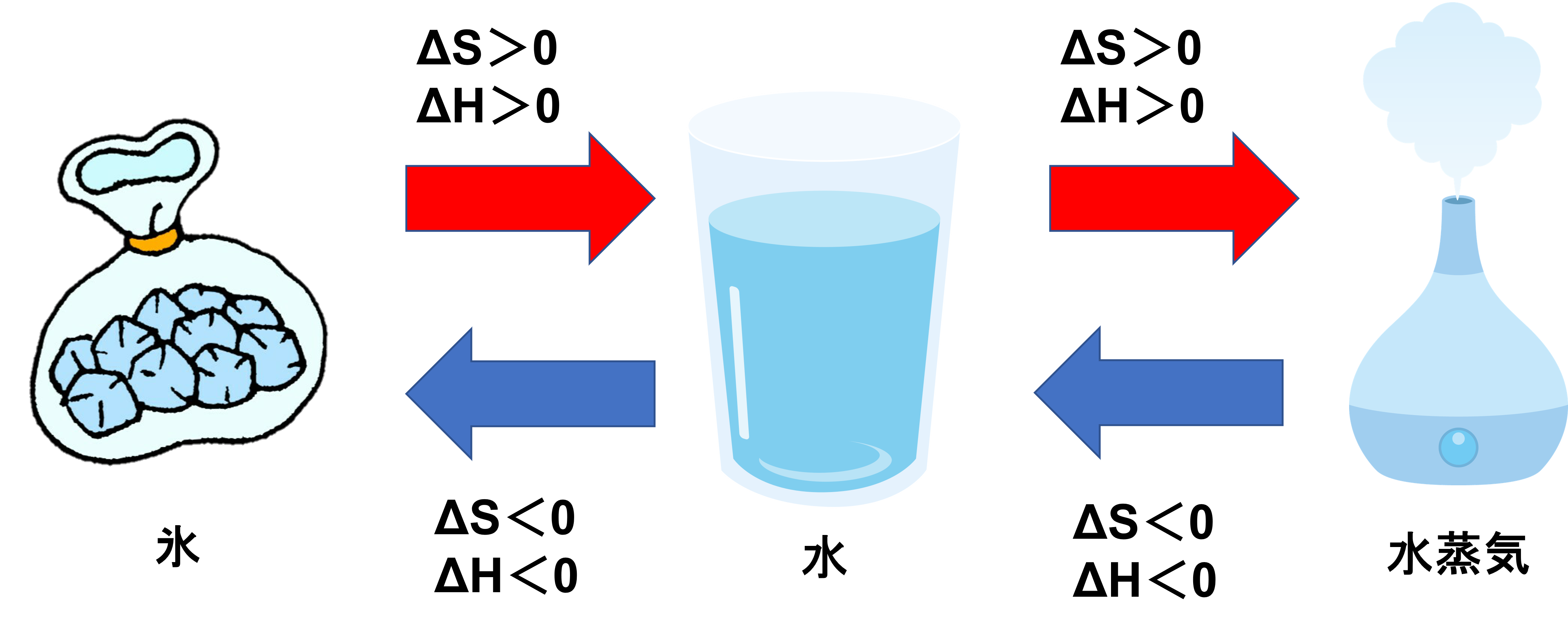
この式より、ギブズ(Gibbs)エネルギーの変化量はΔH、T、ΔSなどによって決まってくることがわかります。さらに定温条件とするとTは固定されるため、ΔH、ΔSに依存してくることがわかり以下の組み合わせがあることがわかります。

 

1. ΔHがマイナス、ΔSがプラス；ΔGはマイナス
2. ΔHがマイナス、ΔSがマイナス；TによってΔGがプラスにもマイナスにもなる
3. ΔHがプラス、ΔSがプラス；TによってΔGがプラスにもマイナスにもなる
4. ΔHがプラス、ΔSがマイナス；ΔGはプラス

 

1についてはΔHがマイナスであるため発熱をしながら、ΔSがプラスで乱雑さが増えていくことを意味するので、自然に起こりやすいことがわかります。また4についてはΔHがプラスであるため吸熱しながら、ΔSがマイナスで乱雑さが減っていくことを意味するので、自然におこりにくいことがわかります。このことから、ΔGはマイナスに行くことが自然であることがわかります。

 

ではΔG=0の時はどうでしょうか？

 

ギブズ(Gibbs)エネルギーが0ということは、エンタルピーも束縛エネルギーも0ということになります。つまり系の変化が何も起こっていないことになるので、平衡状態と言えます。

 

まとめ

• ギブズ(Gibbs)エネルギーの変化量は、エンタルピーとエントロピーの変化により決まる。
• ΔGがマイナスになるのが自発的な反応であり、ΔG=0の時は平衡状態を意味する。