

Sponsored Link
製剤、粘弾性とニュートン流動
固体や液体には様々な性質があります。今回は固体や液体の性質について見ていきます。
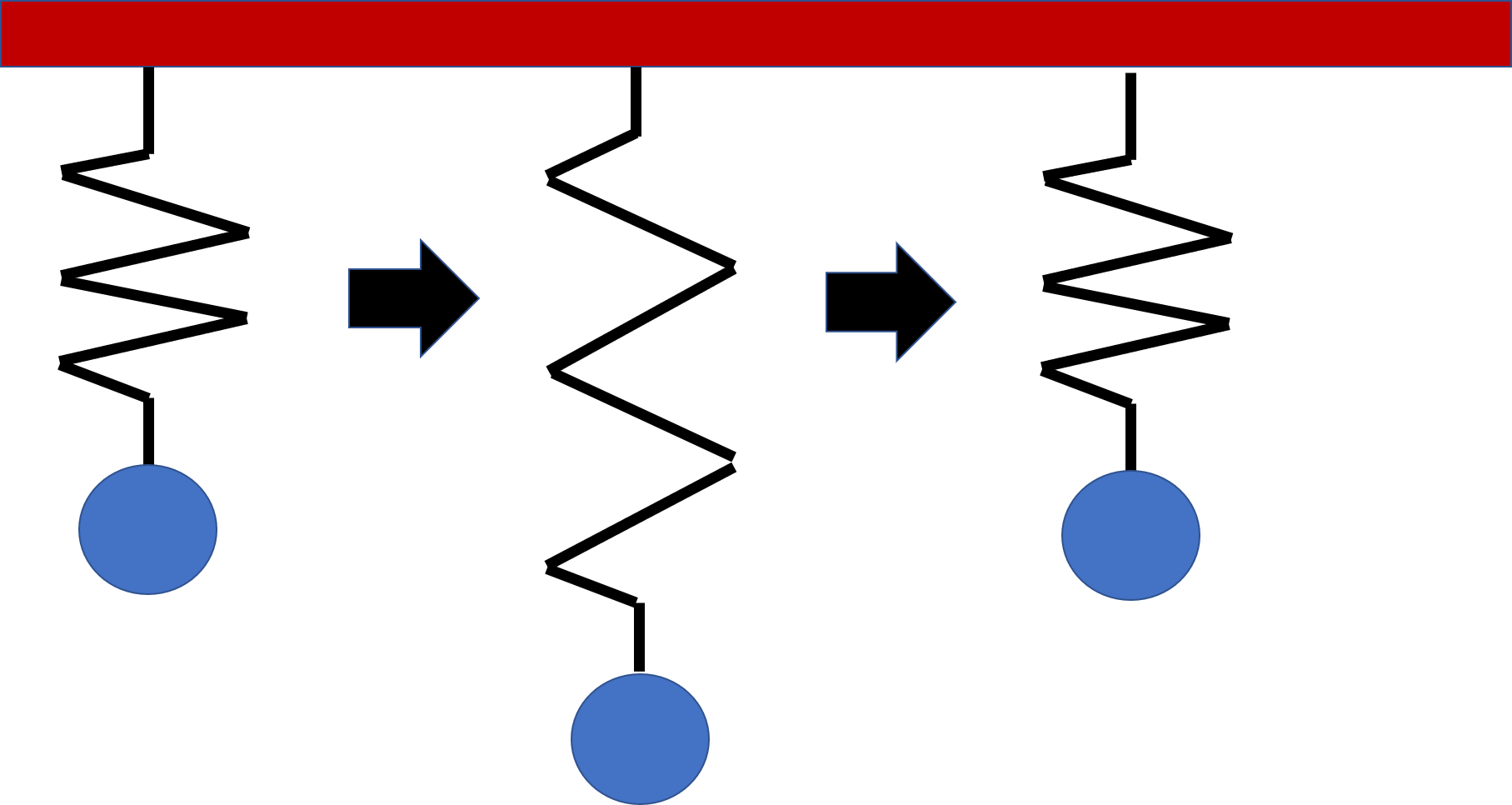
固体に力を加えると、伸びたり変形します。バネをイメージすればわかりやすいですが、バネに重りつけて引っ張って手を離したら元の状態に戻ります。この性質を弾性と言います。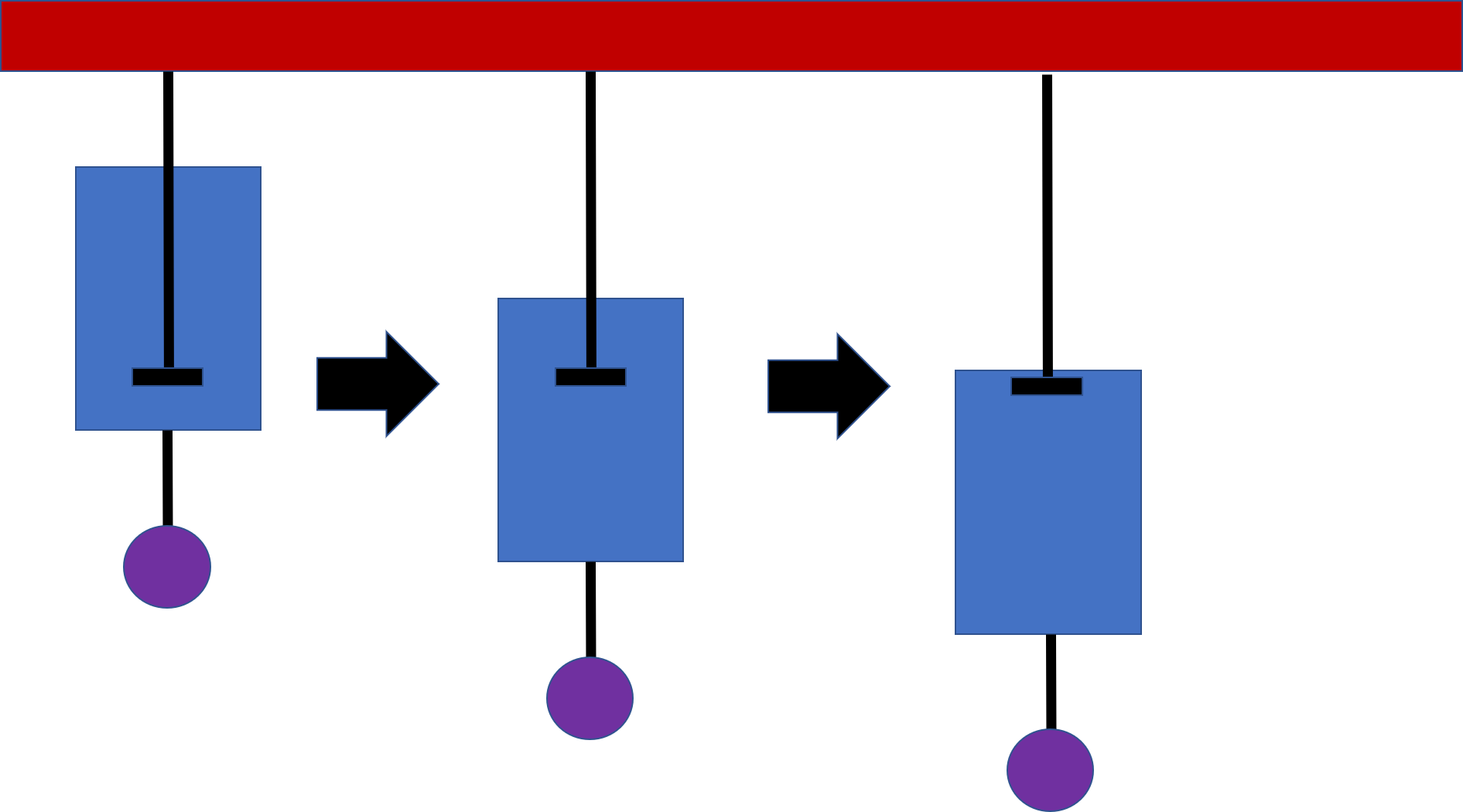
液体の中でもダッシュポットを使い同じような実験をすると、一定速度で伸びて手を離しても元には戻りません。このような性質を粘性と言います。
粘弾性
これらの弾性と粘性の両方の性質を併せ持ったものを粘弾性と言います。軟膏などが粘弾性を持ちます。粘弾性を測定する方法に、Maxwell(マックスウェル)モデルとVoigt(フォークト)モデルがあります。
- Maxwell(マックスウェル)モデル;スプリングとダッシュポットが直列
- Voigt(フォークト)モデル;スプリングとダッシュポットが並列
これもどっちがどっちか混同することがあるので、覚えるコツを。Voigt(フォークト)モデルを、フォークと関連づけましょう。フォークの先端部分は、刺すところが並列して並んでますよね。それを並列と結び付けましょう。Maxwell(マックスウェル)モデルは消去法で解けます。

粘度
面積がAの板に流体を挟み、下の板を固定して、上の板だけ力Fで平行に引っ張ると、下の方と上の方では速度差が生まれます。
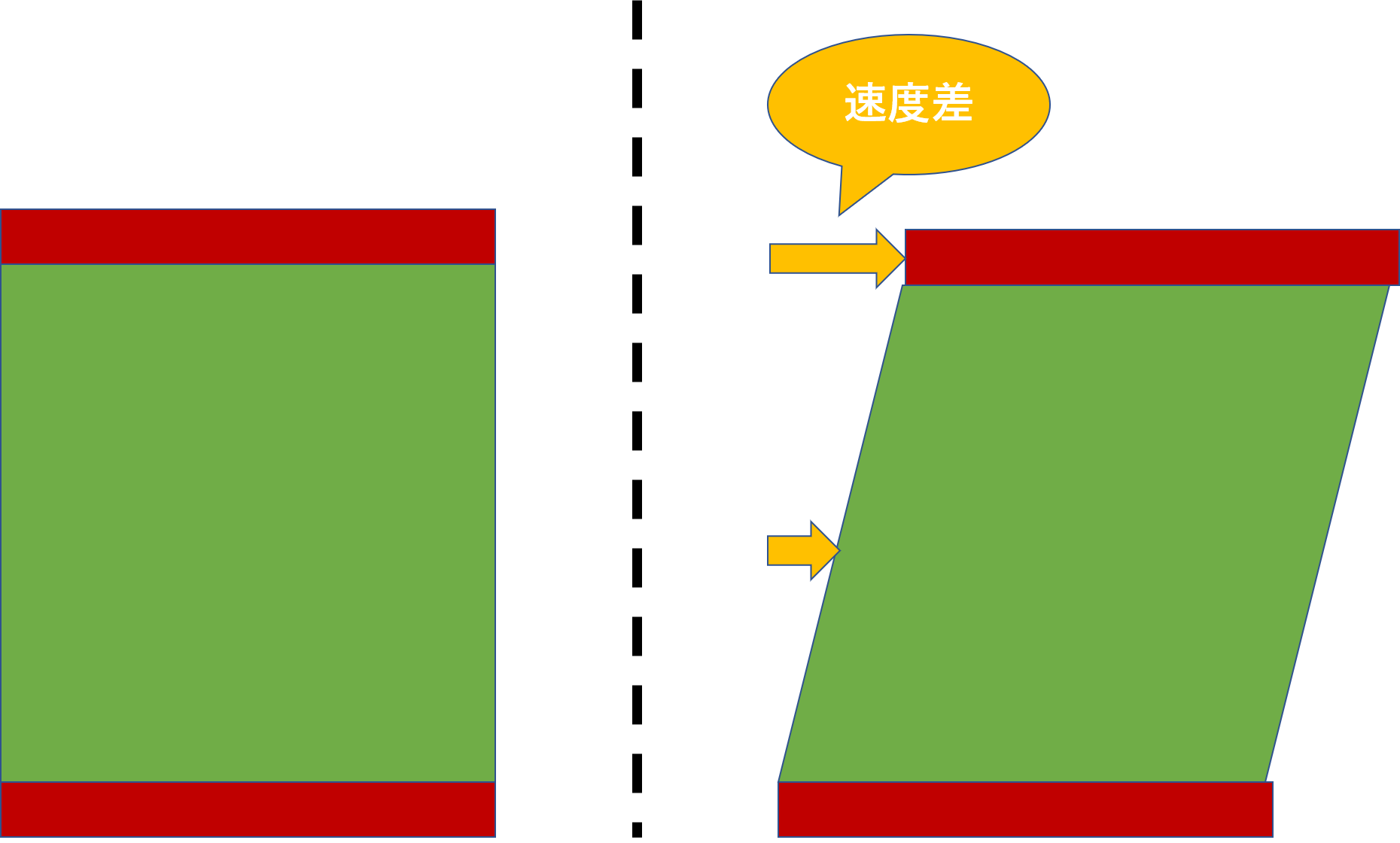
この速度差をずり速度Dと言います。また、この時の単位面積当たりの力(F/A)をずり応力Sと言います。さらに比例定数η(イータ)を粘度とすると
S=η・D
が成り立ちます。これをNewton(ニュートン)の粘性法則と呼びます。そして、Newton(ニュートン)の粘性法則にしたがう流体をニュートン流体と言います。逆にこの法則に従わないものを、非ニュートン流動と言います。
なお粘度の単位はPa・sです。これは高校の物理から単位の計算していけば、導き出せます。
粘度は温度が高くなると減少します。イメージとしては、作り立てで熱いカレーの方がサラサラしているのに対して、一晩寝かせたカレーはプルプルしているかと思います。粘度と温度の関係性はAndrade(アンドレイド)式で表されます。式自体は割愛しますが、Andrade(アンドレイド)式が粘度と温度の関係性を示している式というのは知っておきましょう。
Sponsored Link
Sponsored Link
動粘度
粘度を液体の密度で割ったものを動粘度ν(ニュー)と呼びます。
ν=η/ρ
動粘度の単位はm2/sです。これも単位の計算をすれば導き出せます。
まとめ
- 弾性と粘性を合わせたものを粘弾性という。
- 粘弾性を求める方法にMaxwell(マックスウェル)モデルとVoigt(フォークト)モデルがある。
- Newton(ニュートン)の粘性法則に従うものをニュートン流動、従わないものを非ニュートン流動という。
