薬の分布、結合定数とLangmuir(ラングミュア)式

実習生、新人薬剤師のための参考書＞薬剤のまとめ＞薬の分布、結合定数とLangmuir(ラングミュア)式

薬の分布、結合定数とLangmuir(ラングミュア)式

前回の薬の分布、毛細血管壁と血漿タンパク質に続き、分布をみていきます。前回では薬は非結合形薬物と結合形薬物という2つの形で存在することを話しました。

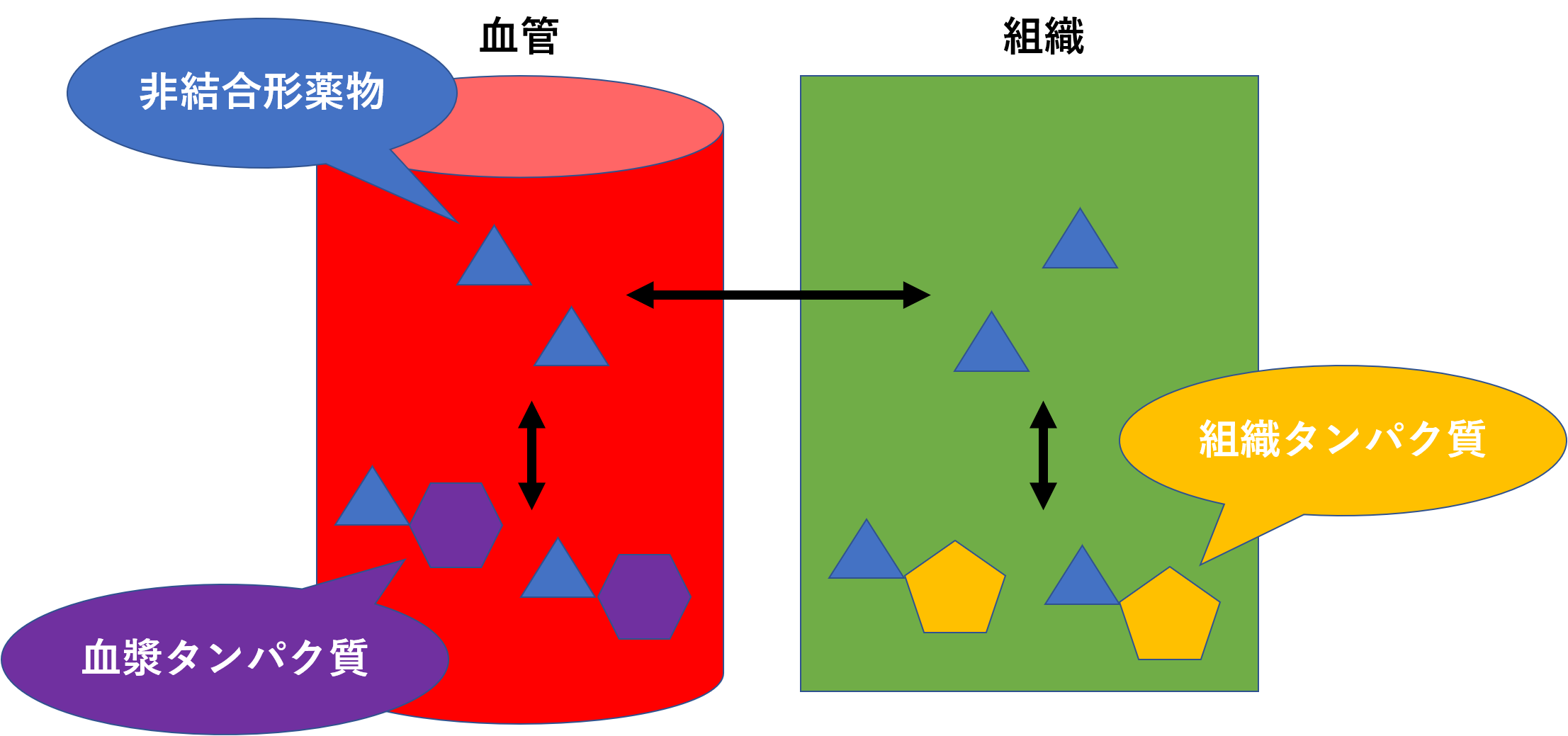
今回は薬がどれくらいタンパクにくっつくかについてまとめていこうと思います。

結合定数

非結合形薬物とタンパク質がくっついて結合形薬物ができ、これは可逆的な反応です。よって、この時の平衡定数をKとすると以下のようにあらわされます。なお、この平衡定数は結合定数と呼ばれます。

この結合定数の測定方法ですが、平衡透析法、限外ろ過法などの方法があります。

限外ろ過法

タンパク質を含んだ薬の溶液を限外ろ過膜と呼ばれる膜を通して遠心分離をかけて測定する方法です。

平衡透析法

平衡透析法は半透膜を用いて行う解析法です。

計算問題が良く出るので、国家試験風の例題を見てみましょう。

ある薬物のアルブミンに対する結合定数を平衡透析法により測定した。袋の中のアルブミン濃度を2.4mmol/L、外液中の薬物初濃度を1.0mmol/Lとして、平衡状態の外液中の薬物濃度を測定したところ0.3mmol/Lだった。結合定数Kはいくらか？

ただしアルブミン1分子あたりの薬の結合部位は1とする。また内液も外液の容積も同じで、薬もアルブミンも容器や膜に吸着しないとする。

平衡透析法の計算問題で抑えるべきポイントは以下の2つです。

平衡状態では内液と外液の非結合形薬物濃度は等しい
タンパク質は膜透過しない

透析前は以下のように図式化できます。

これをもとに見ていきます。まず、ポイント1です。平衡状態の外液中の薬物濃度は0.3mmol/Lだったとあるため、内液の非結合形薬物の濃度も0.3mmol/Lとなります。つまり外液(0.3)と内液(0.3)を合わせると0.6mmol/Lとなります。

次に外液中の初濃度は1.0mmol/Lであり、先ほどの平衡状態での非結合形薬物の外液と内液を合わせたものは0.6mmol/Lであるため、引くと0.4mmol/Lとなります。この0.4mmol/Lがタンパク質とくっついている薬です。

そしてポイント2のタンパク質は膜透過をしないため、内液に2.4mmol/Lアルブミンが存在していることになります。先ほど0.4mmol/Lはタンパク質とくっついていると計算したため、2.4mmol/Lから引くと2.0mmol/Lとなります。これが薬と結合していないフリーのタンパク質となります。

あとは結合定数の式に当てはめるだけです。

K=0.4/(0.3×2.0)=0.667L/mmolが答えです。

Langmuir(ラングミュア)式

平衡透析法の計算で頭がパンクしそうな人はいったん休憩してからみてください(笑)なぜなら、もう1つ結合定数で大事な計算であるLangmuir(ラングミュア)式についてもまとめるからです。

結合定数の式をいじるとLangmuir(ラングミュア)式というものができます。この式は残念ながらクソ暗記してください。ある程度計算問題などをやると覚えてくると思いますが、分子と分母がどっちだっけとなることがあります。そういうのを防止するために、ラング→ランク→rank→r=nkと結び付けると、分子にr=nkがあることは思い出せます。その他のパーツをつけ足して覚えましょう。

このLangmuir(ラングミュア)式をグラフ化したものをDirectプロットと呼びます。さらに、式変形して得られたものがScatchardプロット、両辺逆数プロットと呼びます。

このScatchardプロットと、両辺逆数プロットについて、競合阻害が起きたときにグラフがどう変化するかが国家試験では問われます。ポイントは結合部位数と結合定数がどうなるかです。

薬Aとタンパク質がくっついているところに、競合的な阻害をする薬Bがくると、薬Aが追い出されます。この時薬Aは追い出されたもののタンパク質の部位数は変わっていません。しかし、結合する数は減るため結合定数は下がります。

よって、nは横ばいで、Kは低下するため、それぞれのグラフが以下のようにシフトします。

まとめ

結合定数の測定方法に、平衡透析法、限外ろ過法などがある。
平衡透析法は、平衡状態では内液と外液の非結合形薬物濃度は等しく、タンパク質は膜透過しないのがポイント
Langmuir(ラングミュア)式はグラフと競合阻害時にどうシフトするのかをおさえる。

就職や転職でお悩みの方はコチラ！私はここで年収120万円上がりました

薬の分布、結合定数とLangmuir(ラングミュア)式関連ページ

ADMEと肝初回通過効果の概要: 薬を経口投与した後は、吸収、分布、代謝、排泄といったADMEと呼ばれる流れを受けます。薬を経口投与する際には、肝初回通過効果を受け、一部の薬が代謝されます。
薬の吸収は非撹拌水層、溶解速度、胃内容排出速度などの影響を受ける。: 経口投与された薬は小腸から吸収され、肝初回通過効果を受けます。吸収された薬に影響を与える要因として、非撹拌水層、溶解速度、胃内容排出速度などがあります。
薬の分布、毛細血管壁と血漿タンパク質: 薬の分布では非結合形薬物が組織に移行できます。逆に結合形薬物は血漿タンパク質に薬がくっついています。血漿タンパク質の代表例にアルブミンやα1-酸性糖タンパク質などがあります。
薬の分布、血液脳関門と分布容積: 脳への薬の分布に血液脳関門関わり、脂溶性が高く、分子量が小さいものが血液脳関門を透過しやすいです。分布容積は分布のしやすさを表す指標です。
薬の代謝、CYPの阻害と誘導: 分布した薬は代謝を受けて排泄の準備が行われます。代謝に関わるものにシトクロムP450というものがあり、酸化反応に関わります。CYPは薬によって阻害や誘導を受けます。
薬の排泄は糸球体ろ過、尿細管分泌、尿細管再吸収より行われる。: 薬は胆汁中排泄などもありますが、基本的には糸球体ろ過、尿細管分泌、尿細管再吸収により排泄されます。クレアチニンの腎クリアランスは腎機能の指標となります。
生体膜透過、単純拡散はめんつゆをイメージしよう。: 生体膜透過には、単純拡散などの種類があります。単純拡散はFickの法則により、透過速度は濃度勾配に比例して、膜の厚さに反比例します。またpH分配仮説により分子形が生体膜を透過しやすいです。
特殊輸送、能動輸送はP-糖タンパク質とMichaelis-Menten(ミカエリスメンテン)式をおさえよう。: 特殊輸送は能動輸送、促進拡散、膜動輸送などがあります。能動輸送においては、P-糖タンパク質とMichaelis-Menten(ミカエリスメンテン)式をおさえることが重要です。
薬物動態、消失半減期t1/2とグラフの読み方: 薬物動態を考える際に、消失半減期、分布容積、全身クリアランス、バイオアベイラビリティなどのパラメーターを使います。消失半減期t1/2は血中濃度が半分になるまでの時間です。
薬物動態、分布容積Vdとグラフの描き方: 分布容積Vdは、組織への移行のしやすさを表す指標です。薬物動態では分布容積はDiv=C0・Vdと計算式をあらわすことができます。この式を使って、グラフの描き方を見てみます。
薬物動態、全身クリアランスCLtotとAUC: 薬物動態のうち、CLtot(全身クリアランス)は、単位時間あたりの薬を除去した血液の容積をさします。また、AUC(血中薬物濃度時間曲線下面積)は濃度の合計をさし、CLtot(全身クリアランス)との関係式があります。
薬物動態、腎クリアランスCLrの計算式: 全身クリアランスは腎クリアランスを用いて、CLtot=CLr+CLhとあらわすことができます。また腎クリアランスはCLr・Cp=U・VやCLr=(GFR・fp+分泌クリアランス)(1-R)とあらわすことができます。
薬物動態、腎排泄と尿中排泄率Ae: 薬物動態の尿中排泄率Aeを使うことで、肝代謝か腎排泄かを判断する手掛かりとなります。尿中排泄率Aeを用いて、クリアランスを表すとCLr=CLtot・Aeが成り立ちます。
薬物動態、肝クリアランスCLhと肝抽出率Eh: 薬物動態のうち、肝臓を1回通過した時の薬物濃度の減少率を肝抽出率Ehと言います。また肝クリアランスCLhを用いて、肝抽出率を表すと、CLh=Eh・Qhとなります。
薬物動態、量的バイオアベイラビリティと絶対的バイオアベイラビリティ: 薬物動態のうち経口投与した後、どれくらい利用されるかの割合をバイオアベイラビリティと言います。計算式では、絶対的バイオアベイラビリティ(F)=(AUCpo/Dpo)/(AUCiv/Div)が成り立ちます。
薬物動態、点滴静注と定常状態: 点滴静注を続けると4～5半減期くらいで定常状態に達します。早く定常状態にもっていくために、点滴静注と負荷量(loading dose)を併用することがあります。
薬物動態、繰り返し投与と定常状態: 今までは単回投与を見てきましたが、現実的には繰り返し投与が行われます。繰り返し投与を行っていくと、薬物動態としては定常状態に達します。
薬物動態、抗菌薬のPK/PD、時間依存と濃度依存: PKとPDを組み合わせたものをPK/PDと言います。抗菌薬のPDにはMICやMPCなどがあります。これらのPK/PDや時間依存と濃度依存を考えることで、耐性菌ができにくくなります。
薬物動態、TDMを行う代表的な薬たち: 抗生剤以外にも、一部の薬はより安全に、そして有効に使うためにTDMを行います。TDMはすべての薬で行う必要はなく、行うべき薬の代表例と治療域、中毒症状などをまとめました。
薬物動態、モーメント解析法とMRT: 薬物動態のうち、モデルに基づかない解析法にモーメント解析法があります。モーメント解析法ではAUCやAUMCが使われますが、投与された薬が体に存在する時間MRTなども使います。
製剤、溶解速度とNoyes-Whitney式(ノイエス-ホイットニー式): 薬の溶解度や溶解速度はバイオアベイラビリティに影響を与えます。濃度変化などから溶解速度を求める式にNoyes-Whitney式(ノイエス-ホイットニー式)があります。
製剤、質量変化とHixson-Crowell(ヒクソン-クロウェル式): 質量変化によって、みかけの溶解速度定数Kを求める式がHixson-Crowell(ヒクソン-クロウェル式)です。Hixson-Crowell(ヒクソン-クロウェル式)はシンク条件、粒子径一定の球形粒子が球形を保って溶解することが仮定されています。
製剤、表面張力とGibbs(ギブズ)の吸着吸着等温式: 分子を安定化させて、中へ進ませようとする力を表面張力といいます。溶質の液表面への吸着量と表面張力の関係を表した式をGibbs(ギブズ)の吸着吸着等温式といいます。
製剤、ぬれと接触角: 固体表面に液滴が広がる現象をぬれと言います。ぬれは接触角θによって度合いが表され、拡張ぬれ、浸漬ぬれ、付着ぬれなどに分類されます。Washburn式(ウォッシュバーン式)はぬれに関わる式です。
製剤、界面活性剤と臨界ミセル濃度(c.m.c): 界面活性剤は親油基と親水基からなります。界面活性剤は、様々な特徴を持ち、臨界ミセル濃度(c.m.c)、クラフト点、曇点、HLBなどがあります。
製剤、コロイド分散系の特徴: 分散系は、分子分散系、コロイド分散系、粗大分散系にわけられます。コロイド分散系の特徴は、ブラウン運動、チンダル現象、凝析塩析などがあります。
製剤、懸濁剤や乳剤(エマルション)の特徴: 粗大分散系の代表例には、懸濁剤や乳剤(エマルション)があります。懸濁剤はケーキング、乳剤(エマルション)はクリーミングが起こります。沈降速度はStokes式(ストークス式)に従います。
製剤、粘弾性とニュートン流動: 粘弾性を求める方法にMaxwell(マックスウェル)モデルとVoigt(フォークト)モデルがあります。Newton(ニュートン)の粘性法則に従うものをニュートン流動、従わないものを非ニュートン流動という。
製剤、ニュートン流動と非ニュートン流動のグラフ: ニュートン流動と非ニュートン流動のグラフと、その例を覚えることが重要です。非ニュートン流動には、塑性(ビンガム)流動、準(擬)粘性流動、準(擬)塑性流動、ダイラタント流動(ダイラタンシー)などがあります。
製剤、粒子の測定方法と粒度分布: 粒子の測定方法には、ふるい分け法、沈降法、光学顕微鏡法、コールターカウンター法、気体吸着法、空気透過法などがあります。ふるい分け法、沈降法、光学顕微鏡法、コールターカウンター法からは粒度分布が得られます。
製剤、粉体の充填性、流動性、吸湿性: 粉体の製剤に関わる性質には、充填性、流動性、吸湿性などがあります。充填性はみかけ体積や、みかけ密度、空隙率、流動性は安息角、オリフィスからの流出速度、内部摩擦係数、吸湿性はCRHの理解が大切です。
製剤、結晶多形と粉末X線回析法: 同じ化学物質だが、結晶構造が異なるものを結晶多形といいます。結晶多形の測定方法には、粉末X線回析法があります。粉末X線回析法は、回析されるX線が結晶固有の値であることを利用しています。
製剤、pHと特殊酸塩基触媒作用: H+やOH-によって、薬の分解を促進することを特殊酸塩基触媒作用といいます。特殊酸塩基触媒作用から、分解速度定数を小さくするように、pHをコントロールすることで、薬の分解が最小限に抑えられることがわかります。
製剤、日本薬局方通則のまとめ: 薬の安全性や有効性などの品質を正しく保つために日本薬局方が存在します。今回は日本薬局方のうち、通則についてまとめていきます。
製剤、日本薬局方の散剤のまとめ: 散剤は日本薬局方では、経口投与する粉末状の製剤と定義されています。日本薬局方に載っている散剤の試験法には、製剤均一性試験法、溶出性試験法がある。
製剤、日本薬局方の顆粒剤のまとめ: 日本薬局方で顆粒剤は経口投与する粒状に造粒した製剤と定義されています。日本薬局方の顆粒剤の試験法は、製剤均一性試験法、溶出性試験法又は崩壊試験法などがあります。
製剤、日本薬局方の錠剤のまとめ: 日本薬局方では錠剤は経口投与する一定の形状の固形の製剤と定義されています。日本薬局方では錠剤の試験法は、製剤均一性試験法、溶出性試験法又は崩壊試験法などがあります。
製剤、日本薬局方のカプセル剤のまとめ: 日本薬局方でカプセル剤は、経口投与するカプセルに充?又はカプセル基剤で被包成形した製剤と定義されています。カプセル剤の試験法は、製剤均一性試験法、溶出性試験法又は崩壊試験法などがあります。
製剤、日本薬局方の軟膏剤やクリーム剤のまとめ: 日本薬局方の軟膏剤とクリーム剤のまとめです。軟膏剤や、クリーム剤の基剤には、油脂性基剤、水様性基剤、乳剤性基剤などの種類があり、混合する時には注意が必要です。
製剤、日本薬局方の坐剤のまとめ: 日本薬局方で坐剤は直腸内に適用する体温によって溶融するか、又は水に徐々に溶解若しくは分散することにより有効成分を放出する一定の形状の半固形の製剤と定義されています。坐剤は製剤均一性試験法に適合します。
製剤、日本薬局方のエタノールを含む剤形(酒精剤、チンキ剤、エリキシル剤)のまとめ: 日本薬局方でエタノールを含む剤形には酒精剤、チンキ剤、エリキシル剤があります。酒精剤、チンキ剤、エリキシル剤などのエタノールを含む剤形は気密容器を用います。
製剤、日本薬局方の生薬を含む剤形(チンキ剤、エキス剤、流エキス剤、浸剤・煎剤)のまとめ: 日本薬局方で、生薬を含む剤形の代表例にはチンキ剤、エキス剤、流エキス剤、浸剤・煎剤などがあります。そのうちエキス剤と流エキス剤は重金属試験法に適合する必要があります。
製剤、日本薬局方の甘味を含む剤形(エリキシル剤、シロップ剤、リモナーデ剤)のまとめ: 日本薬局方の甘味を含む剤形には、エリキシル剤、シロップ剤、リモナーデ剤などがあります。エリキシル剤のゴロを抑えれば、シロップは甘いイメージ、リモナーデはレモネードをイメージすれば甘味を含む剤形は抑えられます。
製剤、日本薬局方の無菌の剤形(注射剤、点眼剤、眼軟膏剤)のまとめ: 日本薬局方で無菌で作らなければならない剤形の代表例には、注射剤、点眼剤、眼軟膏剤などがあります。注射剤、点眼剤、眼軟膏剤は無菌試験法に適合する必要があります。
製剤、日本薬局方の滅菌法(最終滅菌法、無菌操作法)のまとめ: 日本薬局方の滅菌法には、最終滅菌法、無菌操作法などがあります。最終滅菌法は製剤を容器に充填した後滅菌します。無菌操作法は原料段階又はろ過滅菌後から、一連の無菌工程により製剤を製造します。
製剤、安定性試験(長期保存試験、加速試験、苛酷試験)のまとめ: 薬の安定性の試験には、長期保存試験、加速試験、苛酷試験などがあります。加速試験はジェネリックの承認審査にも必要です。
製剤、固形製剤の添加剤(賦形剤、結合剤、崩壊剤、滑沢剤): 固形製剤の添加剤には、賦形剤、結合剤、崩壊剤、滑沢剤などがあります。結合剤を抑えれば、崩壊剤も抑えられるので、しっかりと覚えましょう。
製剤、粉砕、混合、造粒に使われる機械: 製剤の工程には粉砕、混合、造粒などがあります。粉砕に使われる機械にはハンマーミル、ボールミル、ジェットミルなどがあります。混合に使われる機械にはリボン型混合機、V型混合機などがあります。
製剤、打錠障害にはキャッピング、ラミネーション、バインディング、スティッキングなどがある。: 単発式打錠機(エキセントリック型打錠機)よりロータリー型打錠機の方が速いです。打錠障害には、キャッピング、ラミネーション、バインディング、スティッキングなどの種類があります。
製剤、輸液の電解質の単位mEq/Lとは?計算方法は?: 輸液の電解質のバランスを見るにはmEq/Lの方がわかりやすいです。mEq/L=mmol/L×電荷数で表され、計算方法などをまとめています。
製剤、浸透圧の単位mOsm/Lとは?計算方法は?: mOsm/L(オスモル)とは、浸透圧の単位です。浸透圧(mOsm)=mmol×分子またはイオンの数で表され、計算方法などをまとめていきます。
製剤、氷点降下度法の計算方法: 水は0℃で凍りますが、塩水では0℃では凍りません、これを利用して等張化計算する方法が氷点降下度法です。血清や涙液や生理食塩水の氷点降下度は0.52℃です。
製剤、食塩当量の計算方法: 食塩当量は血清や涙液は生理食塩水と等張であることを利用して計算します。つまり食塩当量は医薬品の1gが塩化ナトリウム何gの浸透圧と同じかを利用して計算します。
製剤、等張容積法の計算方法: 等張容積は医薬品1gを溶かして結成や涙液と等張にするために必要な水の量を計算します。等張容積法などの計算方法とまとめです。
製剤、コントロールドリリース(放出制御)型製剤にはスパンタブ、ロンタブ、グラデュメット、スパンスル、スパスタブなどがある: コントロールドリリース(放出制御)型製剤のシングルユニットタイプには、スパンタブ、ロンタブ、グラデュメット、マルチプルユニットタイプにはスパンスル、スパスタブなどの種類がある
製剤、薬のキャリアーにはリピッドマイクロスフェアやリポソームなどがある: 薬の有効性や安全性を高めるにはターゲティングが重要です。ターゲティングを実現するにはキャリアーが重要な働きをして、リピッドマイクロスフェアやリポソームなどがあります。

薬剤の結合定数、Langmuir(ラングミュア)式などのまとめ