薬物動態、消失半減期t1/2とグラフの読み方

今までは、ADMEをみてきました。今回から薬物動態をみていきます。薬物動態は時間経過とともに血中濃度がどのように推移していくかなどを見ていきます。

 

 

計算などをしていくうえで、1-コンパートメントモデルというモデルを用います。前回までのADMEのように通常であれば時間をかけて、血中濃度が変化していきますが、1-コンパートメントモデルでは、薬を投与した瞬間に瞬間的に全身に移行すると考えるモデルです。

 

1-コンパートメントモデルでは、以下のような薬物動態パラメーターなどを使っていきます。

 

• 消失半減期；t1/2
• 分布容積；Vd
• 全身クリアランス；CLtot
• バイオアベイラビリティ；F

 

今回は消失半減期を見ていきます。

 

 

消失半減期；t1/2

薬を注射で単回投与したときに、C0という血中濃度に達した後、以下のようなグラフを描き、また数式化できます。

 

 

ここで高校の数学を思い出してください。この数式の自然対数と常用対数をとると以下のようなグラフと数式に変形できます。

 

 

薬を投与した直後の血中濃度をC0とすると、それが半分となるC0/2までの時間を消失半減期と言います。先ほどの自然対数の式のt=t1/2、C=C0/2を代入すると、t1/2=ln2/kelが得られます。

 

このkelを消失速度定数と呼び、大きいほど薬が早く消失していくことになります。片対数グラフの傾きはkelとなります。

 

まだ消失半減期のみしか学んでいないので少し早いですが、国家試験風の問題を見てみましょう。

 

例題

ある薬を100mg静脈内投与したところ、下記の片対数グラフがえられた。この薬のkelはいくらか

 

 

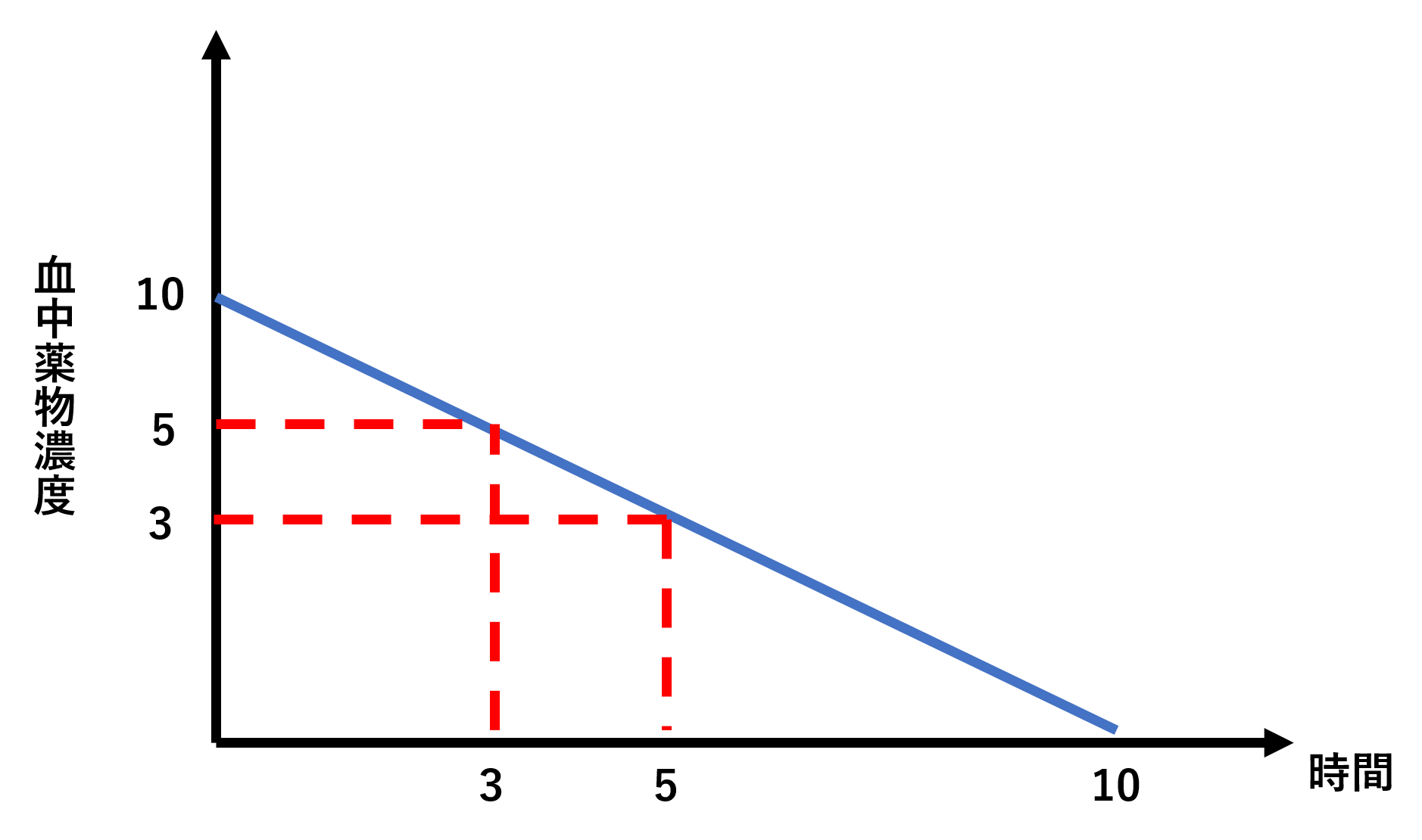
まず縦軸の濃度から見ます。C0が10μg/mlであり、半分の濃度である5μg/mlまで減少する時間を横軸から見ると、3hであることがわかります。つまりt1/2は3hであることがわかります。

 

t1/2=ln2/kelであるため、kel=0.693/3=0.231であることがわかります。

 

 

全身クリアランス(CLtot)を学んだ時にもう一度この問題を見て欲しいのですが、もう一歩進んで全身クリアランスまで求めてみます。

 

Div=C0・Vdであるため、Vd=100/10=10Lと求めることができます。

 

最後に、kel=CLtot/Vdであるため、Cltot=0.231・10=2.31と求めることができます。

 

とりあえず、今回は片対数グラフからkelが求められれば大丈夫です。

 

まとめ

• 薬物動態を考える際に、消失半減期、分布容積、全身クリアランス、バイオアベイラビリティなどのパラメーターを使う。
• 消失半減期t1/2は血中濃度が半分になるまでの時間。
• 片対数グラフの傾きがkelとなる。