

Sponsored Link
生体膜透過、単純拡散はめんつゆをイメージしよう。
薬が効果を示すまでの過程には、生体膜を通過する過程があります。今回は薬がどのようにして生体膜を通過するかをまとめていきます。
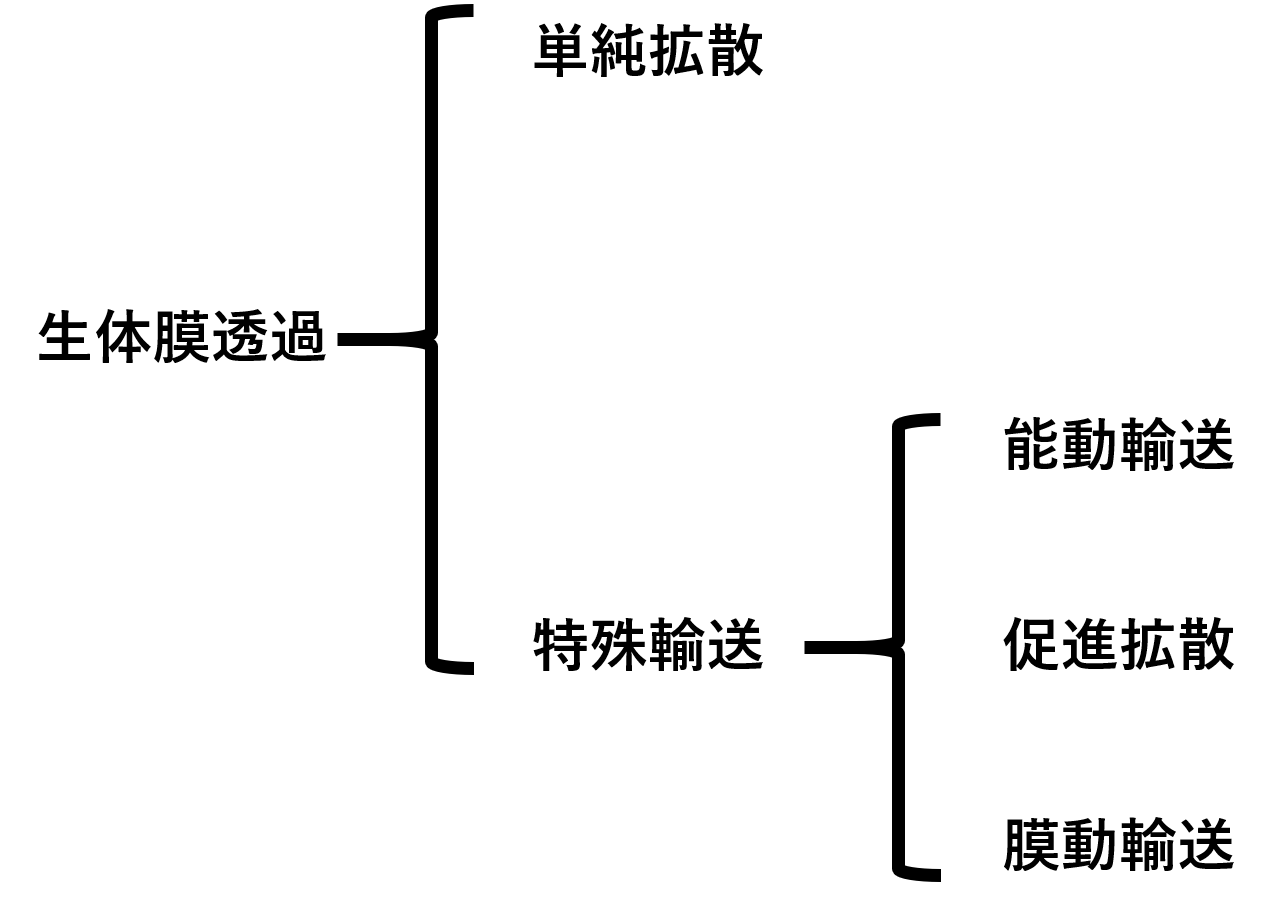
まず大きく分けて、単純拡散と特殊輸送にわけられます。特殊輸送は、さらに能動輸送、促進拡散、能動輸送にわけることができます。
今回はこのうち、単純拡散をまとめていきます。
単純拡散
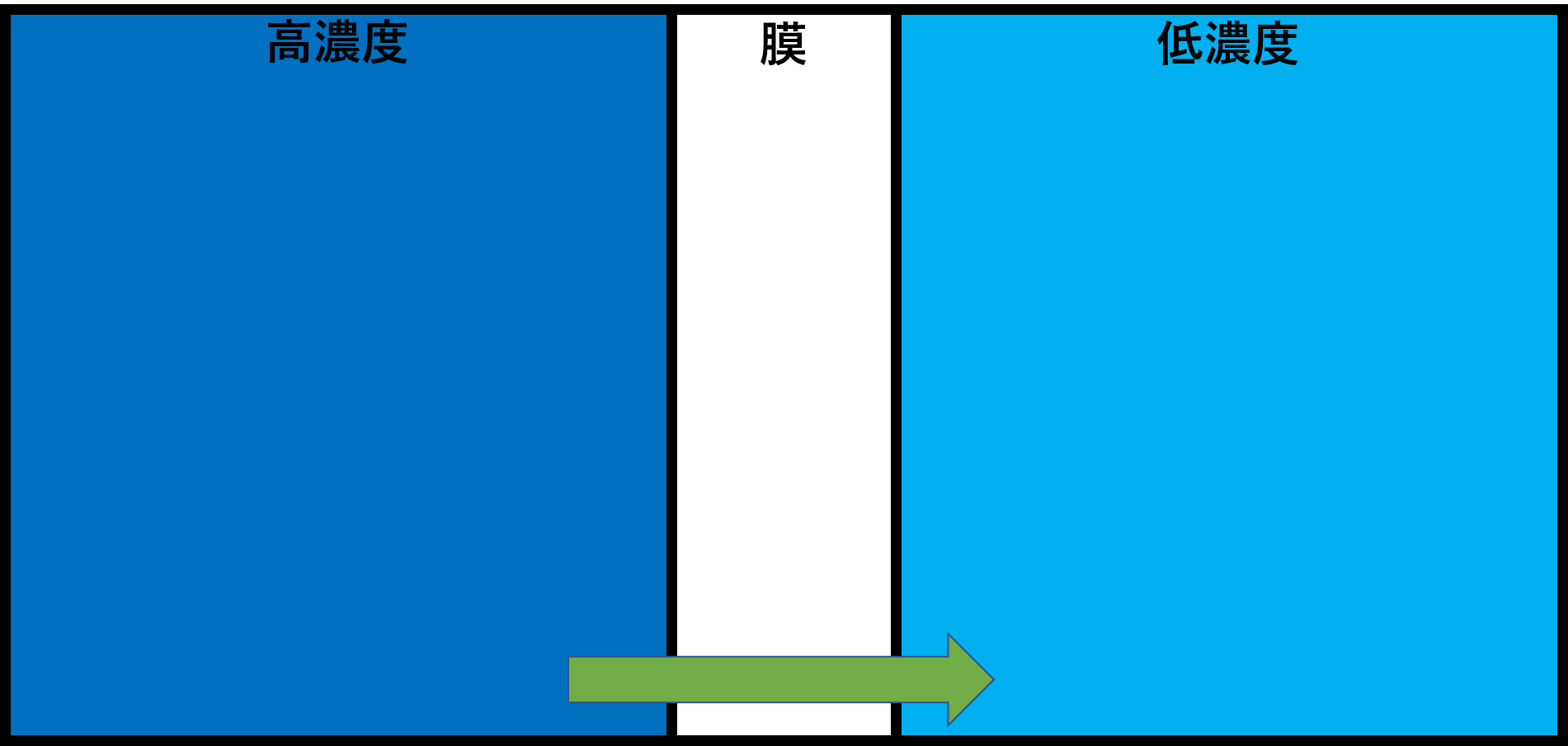
私たちがそうめんを食べるときに、めんつゆを水で薄めるときありますよね?濃いめんつゆに、水を入れると、かき混ぜる動作はありますが基本的に均一になっていい濃さのそうめんのつゆができます。つまりここで言いたいのは、濃いものが薄い方へ移動していくということです。

この現象は生体膜でも区切ってても起こり、高い濃度から薄い濃度へと移動します。これを単純拡散と言います。単純拡散は自然の摂理にかなっているため、次回紹介する担体やATPのエネルギーを必要としません。
そして、単純拡散を考える上で、大事なことが2つあります。それは、Fickの法則と、pH分配仮説です。
Fickの法則
Fickの法則を定義的に言うとするならば、単位面積当たりの拡散速度は濃度勾配に比例するとなります。
難しい法則が出てきたなと感じるかもしれませんが、さっきの濃いところから薄いところに移動する拡散速度を法則化したのがFickの法則です。
国家試験では、透過速度が何に比例するか、反比例するかで引っ掛けてきます。さっきのめんつゆの内容がわかっていれば大したことはありません。
まず透過速度は濃度勾配に比例します。濃いめんつゆの方がより早く拡散するイメージです。
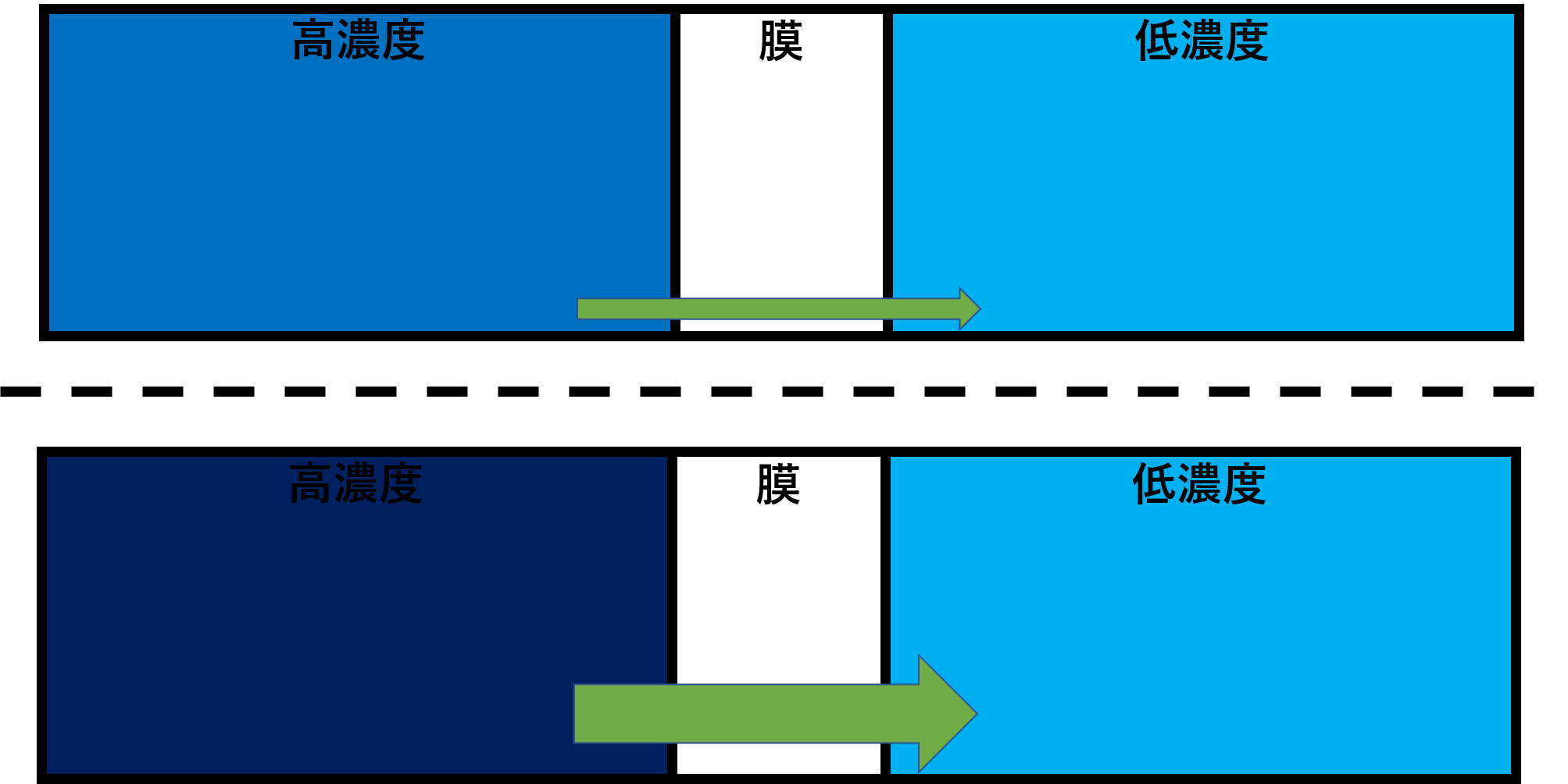
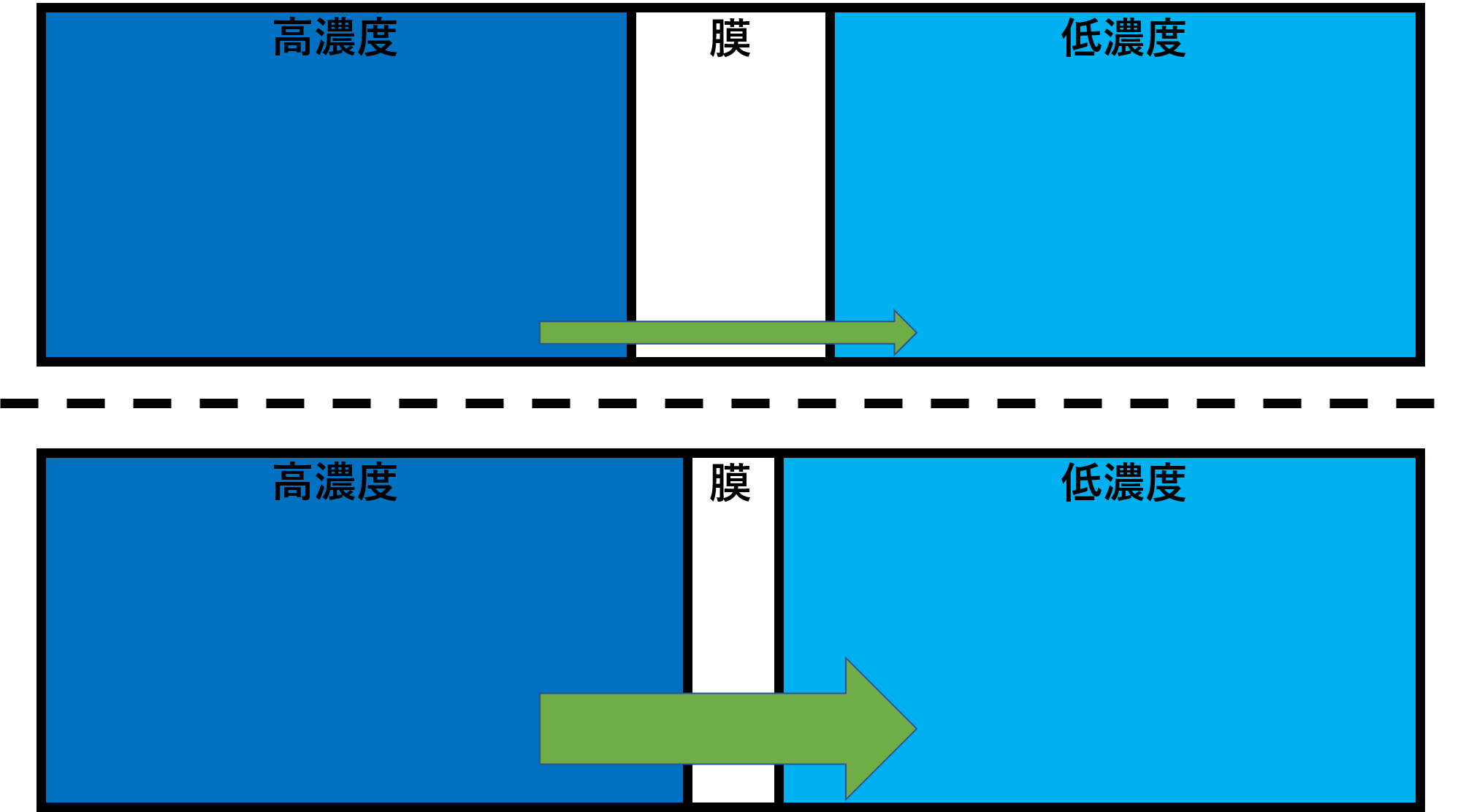
次に透過速度は膜の厚さに反比例します。膜が厚ければ、それだけ障害物があるわけですから、時間がかかるイメージです。
pH分配仮説
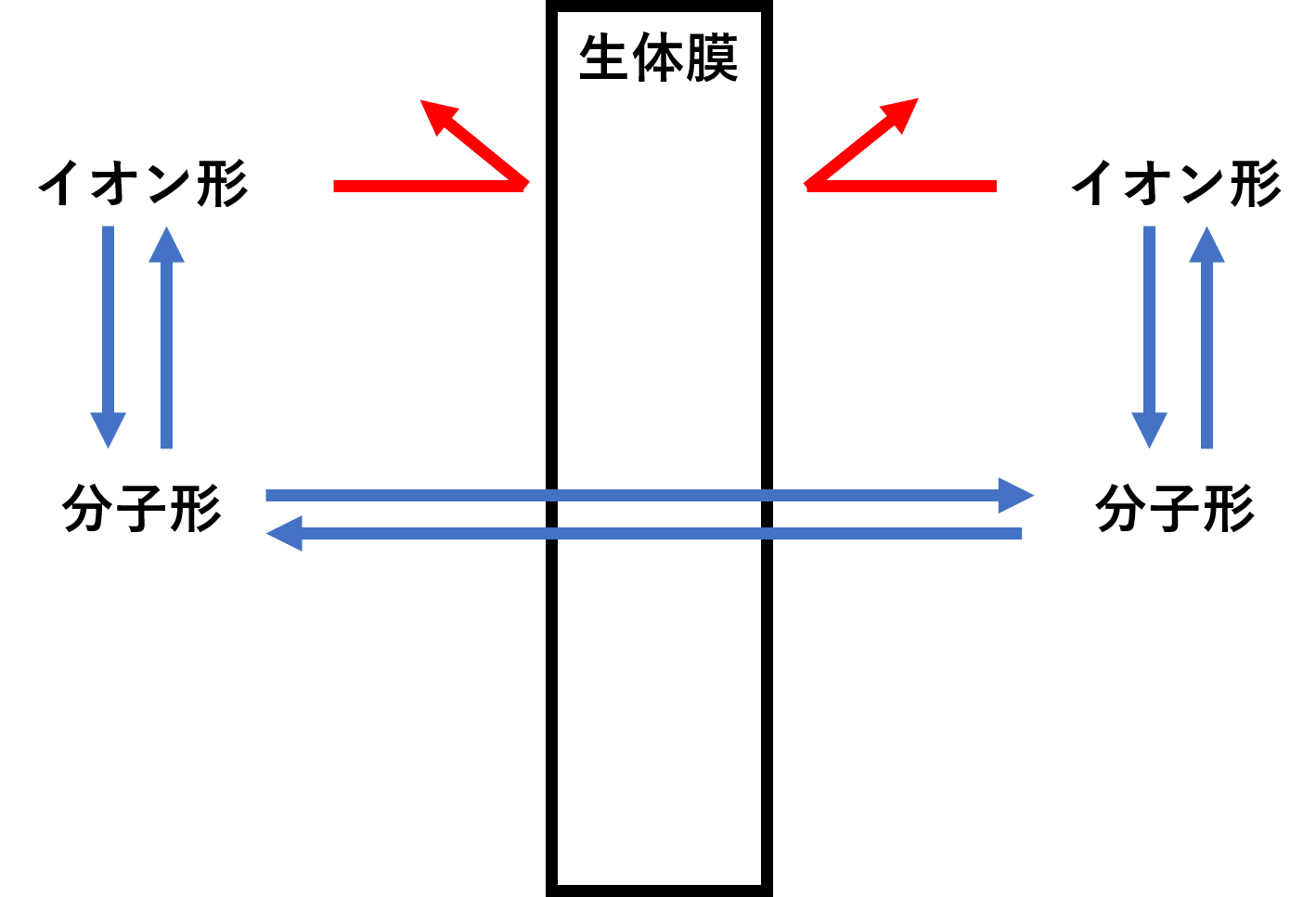
薬は存在するpHの環境によって、分子形や、イオン形といった形をとります。
生体膜がもし完全な脂質膜で構成されているならば、薬の透過性はそのpHにおける分子形の存在割合などによって決まります。これをpH分配仮説と言います。
これも良くわからないと思うので、少しかみ砕きます。まず、水と油は混ざりにくいですよね。逆に塩に水はよく溶けます。

水を仲介すると、油と塩は仲が悪いわけです。塩は水に溶けると、Na+とCl-のイオンとなります。生体膜は同じ油と考えると、塩水(イオン形)は反発して透過できないことになります。
逆に油同士は仲がいいことをイメージできれば、分子形が生体膜を通過しやすいのをイメージできると思います。
薬の膜透過において、分子形とイオン形の比はHenderson-Hasselbalch(ヘンダーソンハッセルバルヒ)式で計算できます。この式は、弱酸性の薬か、弱塩基性の薬かによって式が異なるため注意が必要です。両方覚えようとすると、こんがらがることがあるため、個人的には、弱酸性だけしっかり覚えて、弱塩基性はその逆と覚えるのをオススメします。
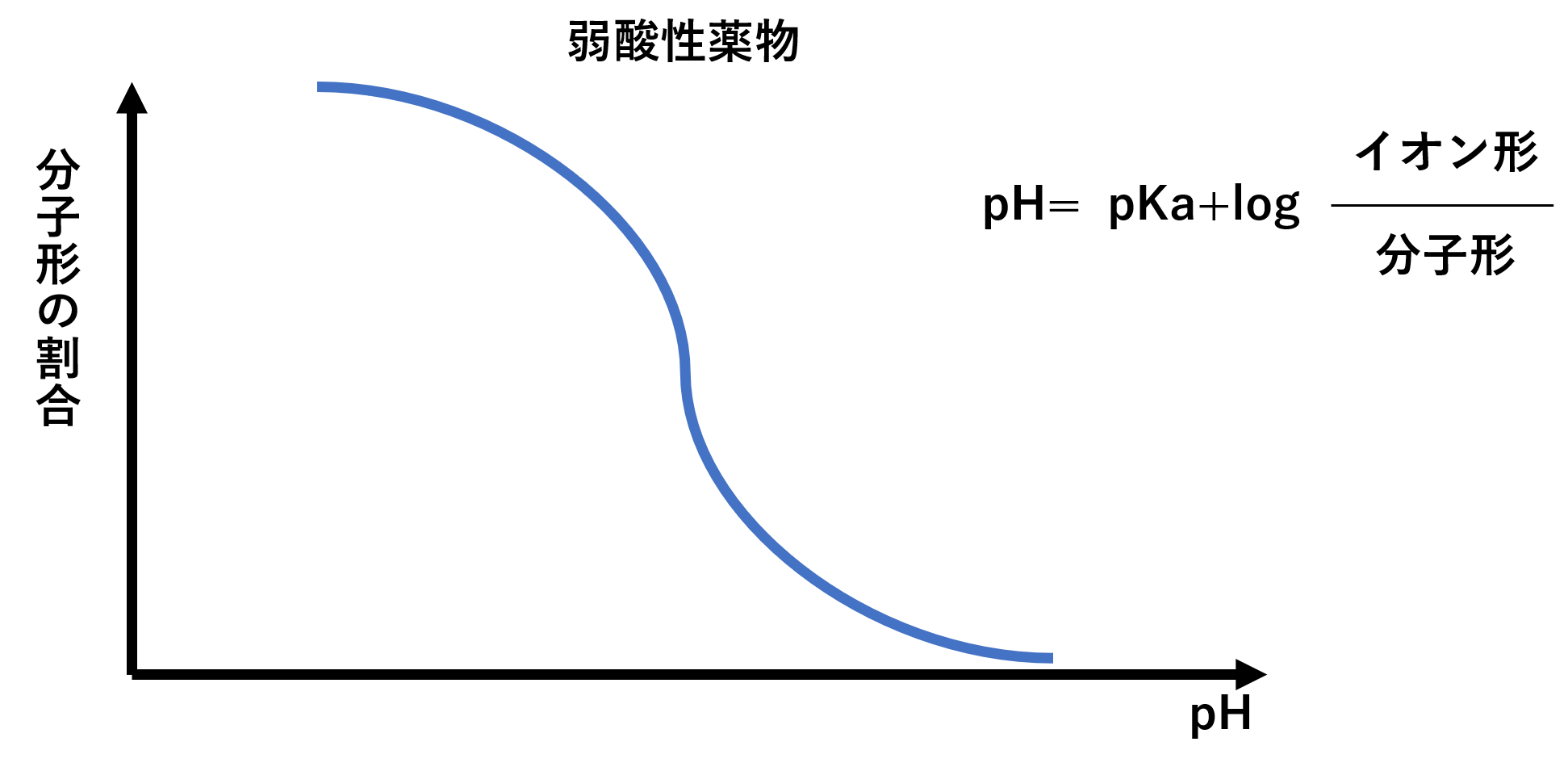
さて、この式ですが、2種類の弱酸性の薬を比較したときに定数であるpKaが大きい方が透過性が良いというのが国家試験で問われます。
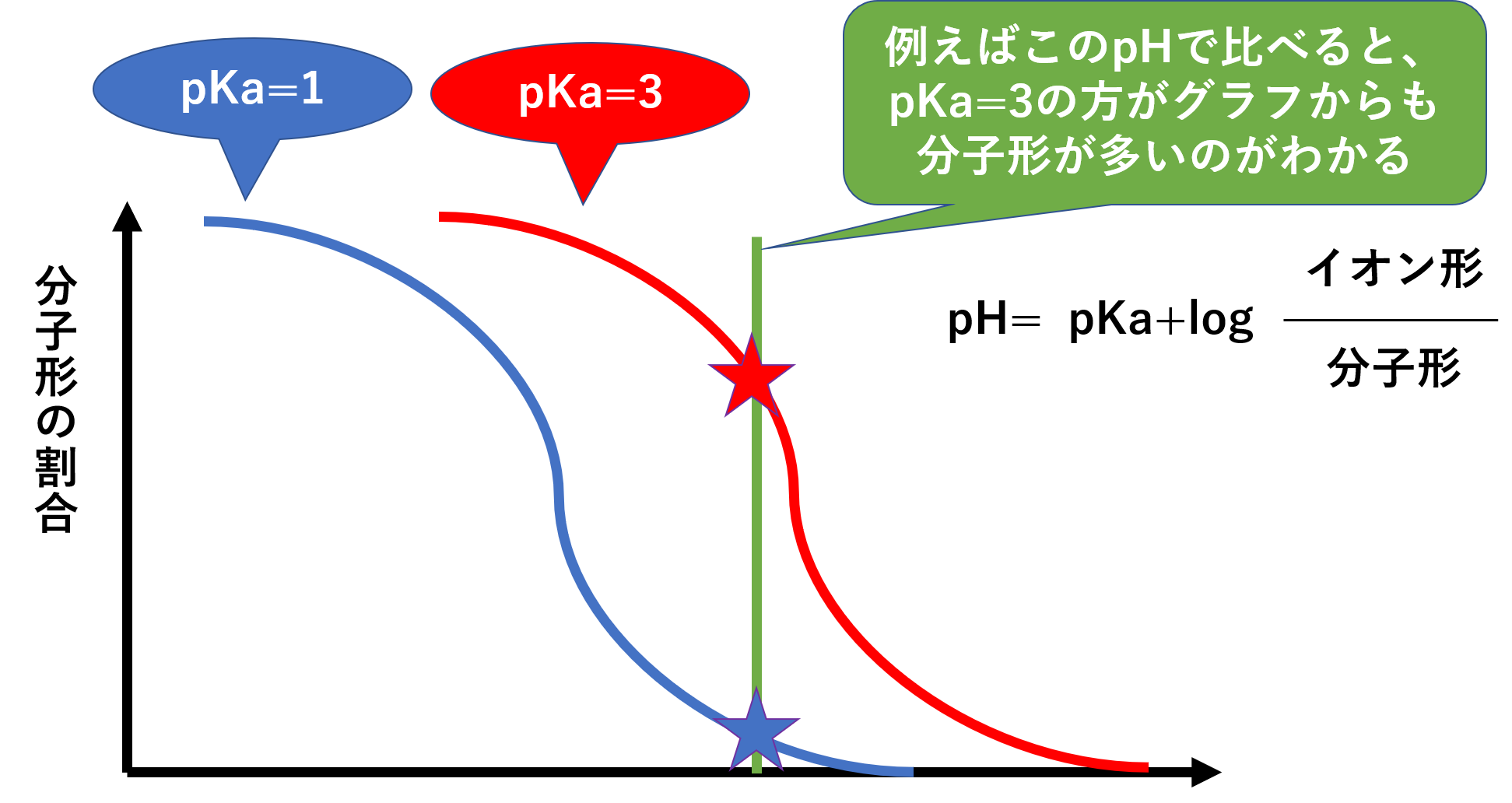
式さえ覚えていれば、高校の数学を思い出して、具体例を当てはめるだけですぐにわかります。例えばpKa=1とpKa=3の薬を比べてみましょう。
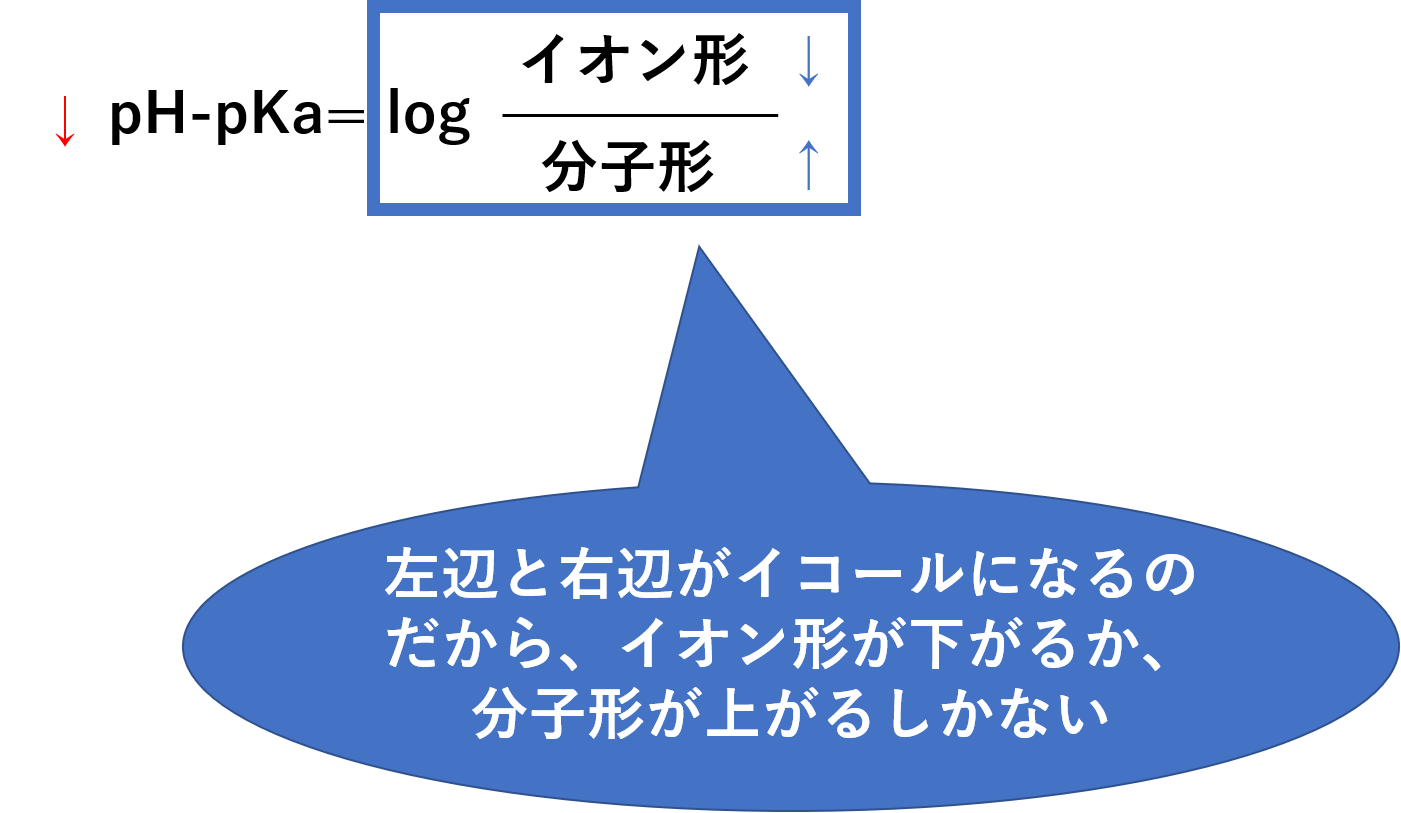
pH-pKa=log(イオン形)/(分子形)となります。左辺はpKa=3の時の方が少ないことがわかります。
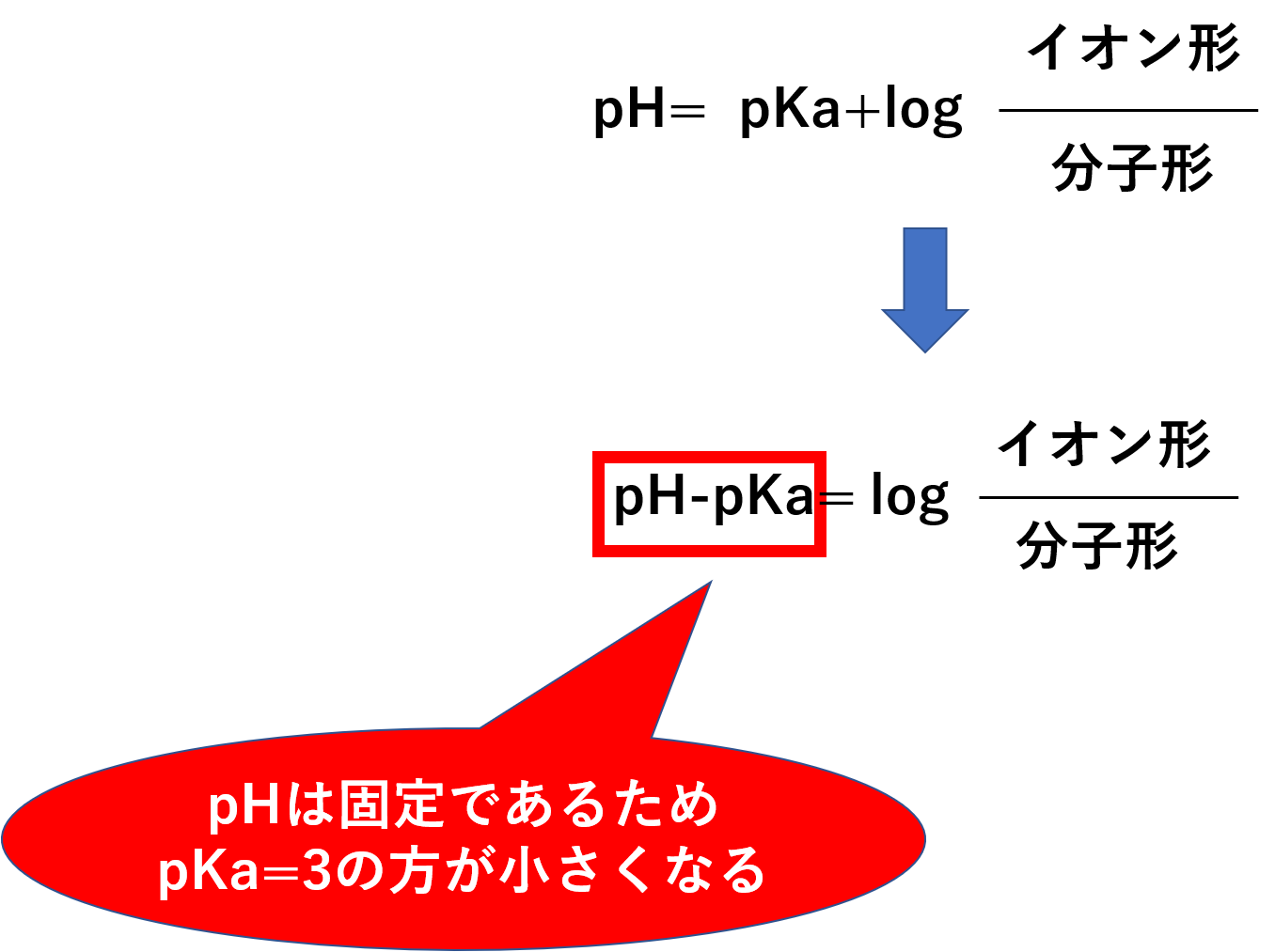
そうすると、それとイコールになる右辺も必然的に少なくなります。右辺の中だけで考えるとするならば、右辺を少なくするには、イオン形を下げるか、分子形を上げるしかありません。つまり分子形が上がるわけです。分子形が上がるということは膜の透過性が上がるということになります。
冒頭の話に戻りますが、私はめんつゆは濃い方が好きです。大事なので最後に主張させてもらいました(笑)次回は特殊輸送についてまとめていきます。
まとめ
- 単純拡散は濃い方から薄い方へ移動する。
- Fickの法則により、透過速度は濃度勾配に比例して、膜の厚さに反比例する。
- pH分配仮説により、分子形が生体膜を透過しやすい。
