Fischer投影式の考え方

前回の立体異性体、エナンチオマーとジアステレオマーでは立体異性体について見ました。今回はFischer投影式について見ていきたいと思います。

 

 

Fischer投影式

Fischer投影式の説明をするにあたって、思い出して頂きたいことがあります。それは混成軌道などからなる構造式は角度を持つということです。角度を持つ構造式を紙の上に平べったく書くのには限界があります。

 

例えば、以下の構造式は紙の上では平べったく書かれていますが、本当であれば以下のような形をとっています。

 

 

以前から当たり前のように使っていますが、太い三角形の単結合は紙のある平面より手前側に出ていることを示します。逆に点線の太い三角形の単結合は紙のある平面より奥側にあることを示します。Fischer投影式はこれを用いて立体的に構造式を表現する方法になります。

 

立体空間把握能力が重要なので早速例題で見ていきます。Fischer投影式も習うより慣れよです(笑)

 

 

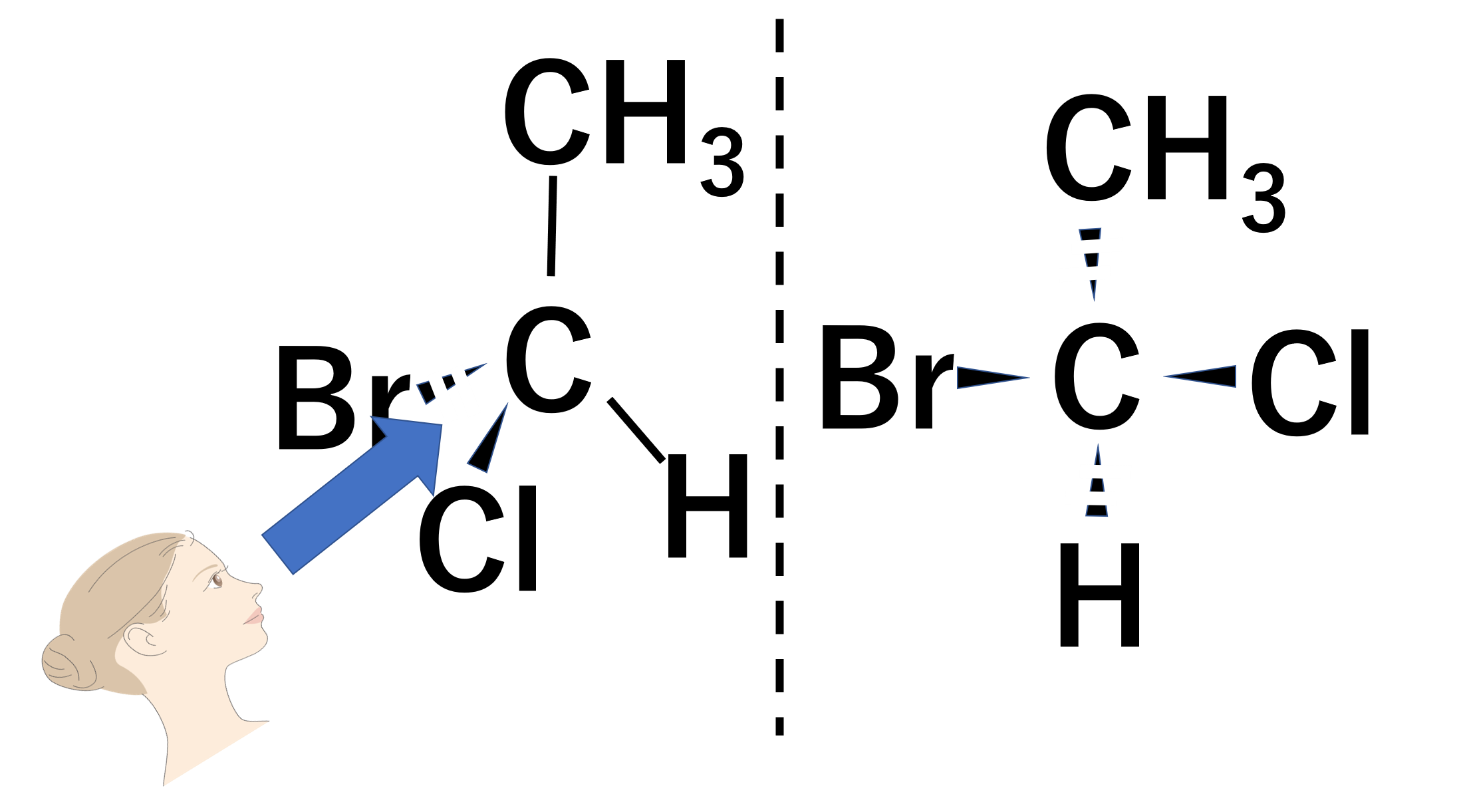
例題1

次の構造式をFischer投影式で書け

 

 

先ほどの説明の構造式となんら変わりません。Fischer投影式では下の図の位置から構造式を見ると、右と左の単結合が手前に伸びています。上と下の単結合が奥に伸びています。よって以下のFischer投影式が答えです。

 

 

例題2

次の構造式をFischer投影式で書け

 

 

最初の構造式が先ほどとは違います。平面上にあるのは、CH3-C-C-CH3となります。平面より手前に出ているのは左側のHと右側のClです。平面より奥にあるのは、左側のBrと右側のHです。

 

さてFischer投影式では上と下は平面より奥側に、右と左は手前側に書く必要があります。そのため問題の構造式ではFischer投影式を描くにはバラバラしている状態となっています。よってまずこれをFischer投影式を描きやすい形に整えます。

 

 

やり方はどうでもいいのですが、今回は左側を固定して右側を180°回転させます。そうすると次のような構造式となります。これで準備OKです。

 

 

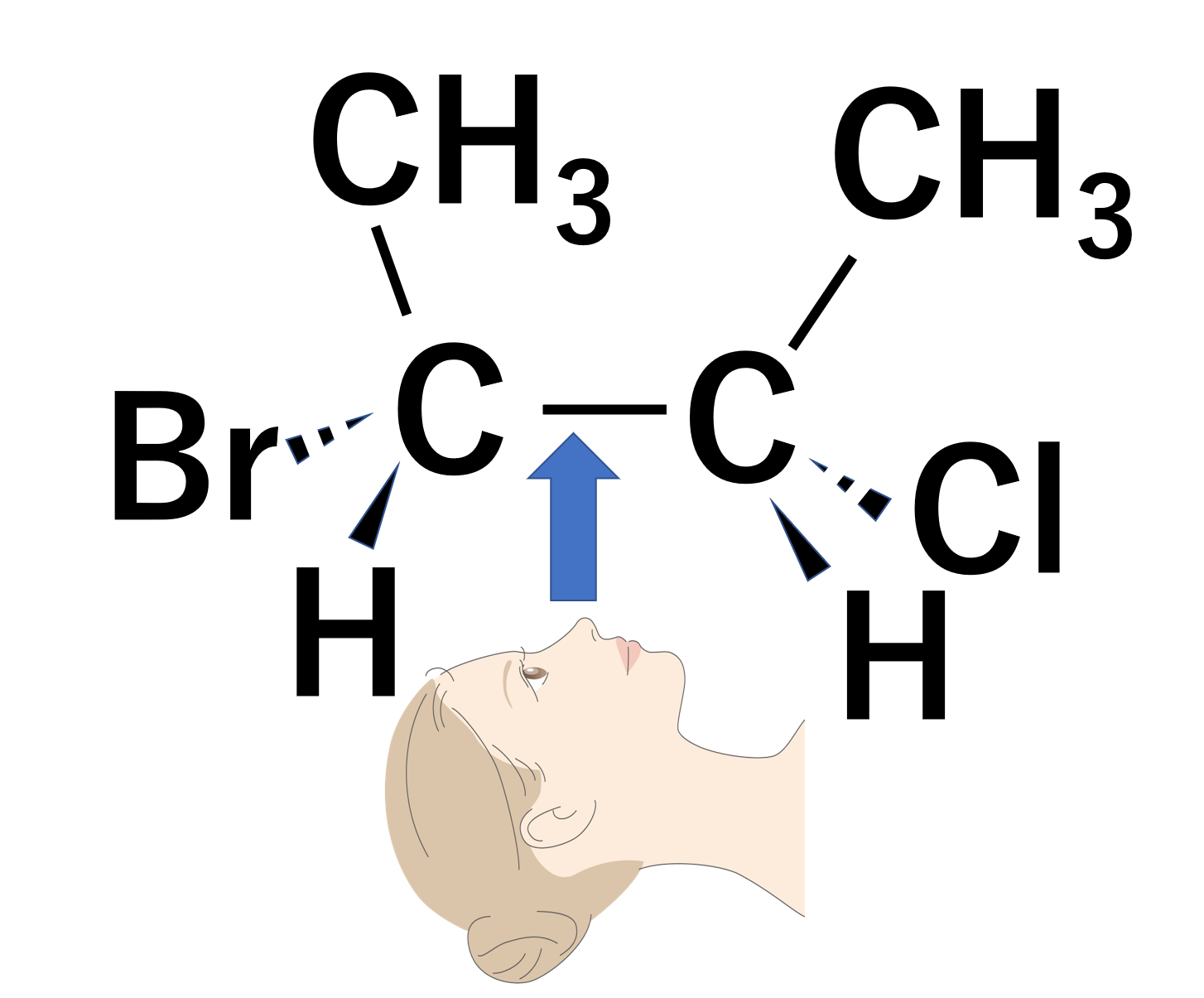
回転させた構造式を下から見て縦にするイメージです。そうすると、メチル基が平面から奥側にある状態となり、その他の側鎖は手前側に出ている状態となります。

 

よって以下のFischer投影式が答えとなります。

 

 

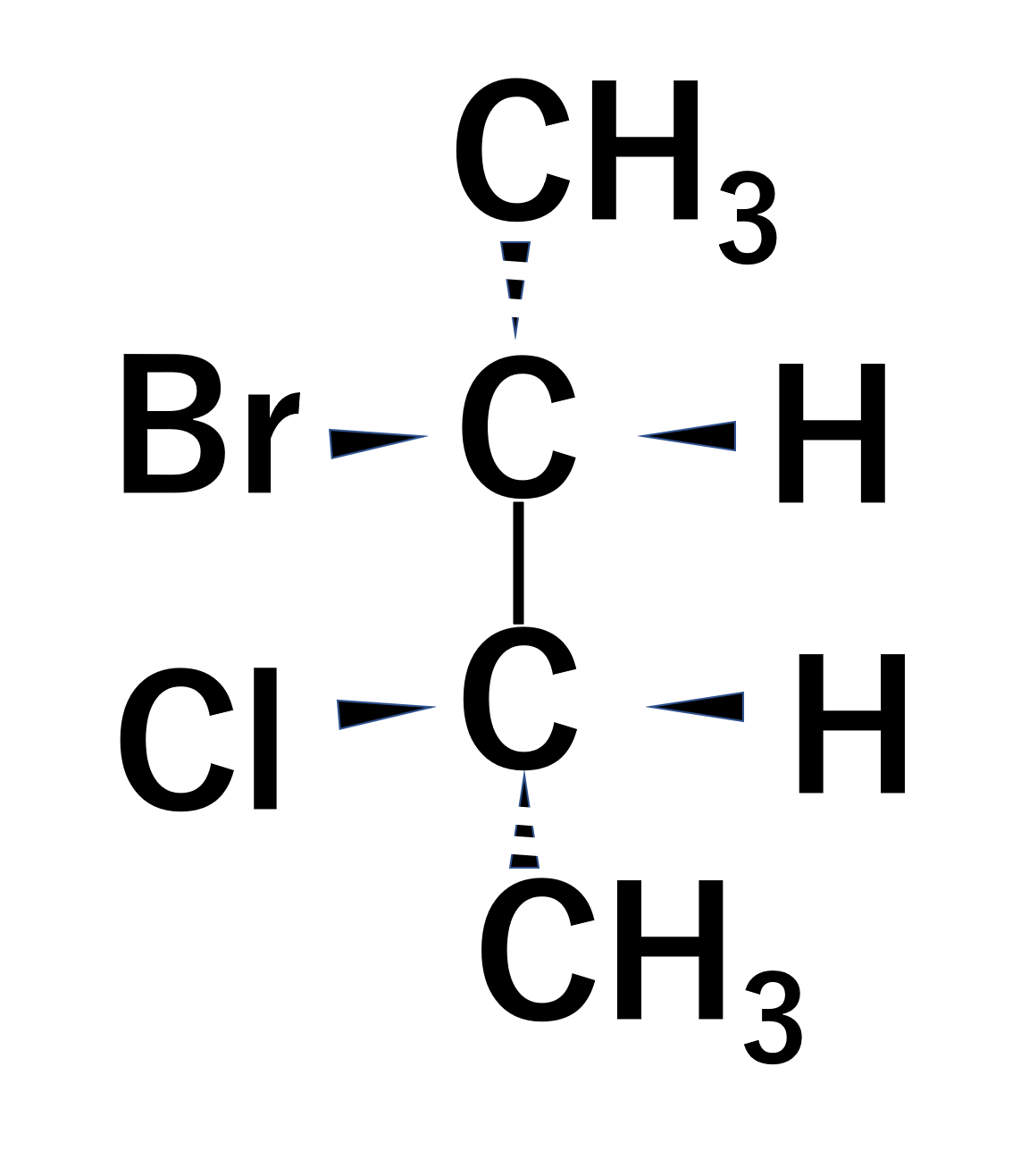
Fischer投影式は立体空間把握能力が大事なので頭の中でできる人はいいですが、苦手な人はしっかり紙に書いて考えましょう。

 

まとめ

• Fischer投影式を書くときには、上下左右を回転させて合わせてから描く。